
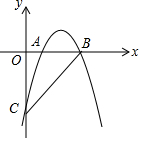
 已知抛物线y=-x2+4x-3经过A(1,0),B(3,0),点C(0,-3),在抛物线上是否存在一点P,使得∠PCB>∠ACB,若存在,求出P点的横坐标的取值范围.
已知抛物线y=-x2+4x-3经过A(1,0),B(3,0),点C(0,-3),在抛物线上是否存在一点P,使得∠PCB>∠ACB,若存在,求出P点的横坐标的取值范围. 分析 分点P在点A左侧和右侧考虑.①观察图形可知,当点P在点A的左侧且不于点C重合时,∠PCB>∠ACB,由此可得出x<0或0<x<1;②当点P在点A的右侧时,作点A关于直线BC的对称点A′,连接A′B,连接CA′交抛物线与点E,根据点A的坐标可找出点A′的坐标,由点C、A′的坐标利用待定系数法可求出直线A′C的解析式,再联立直线A′C和抛物线解析式成方程组,通过解方程组即可得出点E的坐标,结合图形即可找出当x>113时,∠PCB>∠ACB.综上即可得出结论.
解答 解:分两种情况考虑:
①当点P在点A左侧且不于点C重合时,观察图形可知,∠PCB>∠ACB,
∴x<0或0<x<1;
②当点P在点A的右侧时,作点A关于直线BC的对称点A′,连接A′B,连接CA′交抛物线与点E,如图所示.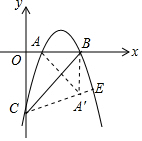
∵点B(3,0),点C(0,-3),点A(1,0),
∴∠OBC=45°,AB=3-1=2.
∵点A、A′关于BC对称,
∴AB=A′B,∠ABC=∠A′BC,
∴∠ABA′=2∠ABC=90°,
∴A′(3,-2).
设直线A′C的解析式为y=kx+b(k≠0),
将C(0,-3)、A′(3,-2)代入y=kx+b,
$\left\{\begin{array}{l}{b=-3}\\{3k+b=-2}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=\frac{1}{3}}\\{b=-3}\end{array}\right.$,
∴直线A′C的解析式为y=$\frac{1}{3}$x-3.
联立直线A′C和抛物线解析式成方程组,
$\left\{\begin{array}{l}{y=\frac{1}{3}x-3}\\{y={-x}^{2}+4x-3}\end{array}\right.$,解得:$\left\{\begin{array}{l}{{x}_{1}=0}\\{{y}_{1}=-3}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=\frac{11}{3}}\\{{y}_{2}=-\frac{16}{9}}\end{array}\right.$,
∴点E($\frac{11}{3}$,-$\frac{16}{9}$),
∴当x>$\frac{11}{3}$时,∠PCB>∠ACB.
综上所述:在抛物线上是否存在一点P,使得∠PCB>∠ACB,P点的横坐标的取值范围为x<0或0<x<1或x>$\frac{11}{3}$.
点评 本题考查了二次函数图象上点的坐标特征、待定系数法求一次函数解析式以及等腰三角形的性质,依照题意画出图形,利用数形结合解决问题是解题的关键.


科目:初中数学 来源: 题型:解答题
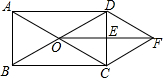 如图所示,在矩形ABCD中,对角线AC,BD相交于点O,E是CD的中点,连接OE,过点C作CF∥BD交线段OE的延长线于点F,连接DF.求证:
如图所示,在矩形ABCD中,对角线AC,BD相交于点O,E是CD的中点,连接OE,过点C作CF∥BD交线段OE的延长线于点F,连接DF.求证:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
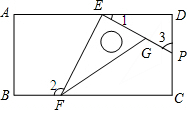 如图,一个含有30°角的直角三角板的两个顶点E、F放在一个长方形的对边上,点E为直角顶点,∠EFG=30°,延长EG交CD于点P,如果∠3=65°,那么∠2的度数是( )
如图,一个含有30°角的直角三角板的两个顶点E、F放在一个长方形的对边上,点E为直角顶点,∠EFG=30°,延长EG交CD于点P,如果∠3=65°,那么∠2的度数是( )| A. | 100° | B. | 105° | C. | 115° | D. | 120° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
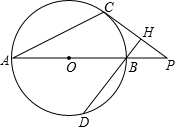 如图,C为⊙O上的一点,P为直径AB延长线上的一点,BH⊥CP于H交⊙O于D,∠PBH=2∠PAC.
如图,C为⊙O上的一点,P为直径AB延长线上的一点,BH⊥CP于H交⊙O于D,∠PBH=2∠PAC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (m-2)(m+2)=m2-2 | B. | (x-6)(x+6)=x2+36 | C. | (x-y)(x+y)=x2-y2 | D. | (x+y)(x+y)=x2+y2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{600}{x}=\frac{600}{(1+20%)x}-2$ | B. | $\frac{600}{x}=\frac{600}{(1+20%)x}+2$ | ||
| C. | $\frac{600}{x}=\frac{600}{20%x}-2$ | D. | $\frac{600}{x}+2=\frac{600}{(1+20%)x}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
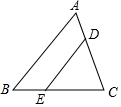 如图所示,△ABC中,点D、E分别是AC、BC边上的点,且DE∥AB,CD:CA﹦2:3,△ABC的面积是18,则四边形ABED的面积是( )
如图所示,△ABC中,点D、E分别是AC、BC边上的点,且DE∥AB,CD:CA﹦2:3,△ABC的面积是18,则四边形ABED的面积是( )| A. | 6 | B. | 8 | C. | 9 | D. | 10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com