�Ķ����в��ϣ��ش����⣮
���ϣ�
��Ʊ�г���������Ʊ��Ҫ�ֱ���ӡ��˰���й�˰�ѣ��Ի���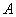 �ɵĹ�Ʊ����Ϊ�������ɱ��Ҫ���ɣ�
�ɵĹ�Ʊ����Ϊ�������ɱ��Ҫ���ɣ�
��ӡ��˰�����ɽ�����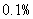 ���㣻
���㣻
�ڹ����ѣ����ɽ�����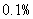 ���㣻
���㣻
��Ӷ�𣺰������ڳɽ�����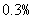 ���㣨���ⰴ
���㣨���ⰴ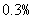 ���㣩������5Ԫ��5Ԫ���㣮
���㣩������5Ԫ��5Ԫ���㣮
����ijͶ������ÿ��5.00Ԫ�ļ۸��ڻ���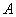 ���������Ʊ����������1000�ɣ���ÿ��5.50Ԫ�ļ۸�ȫ����������ӯ�����٣�
���������Ʊ����������1000�ɣ���ÿ��5.50Ԫ�ļ۸�ȫ����������ӯ�����٣�
�⣺ֱ�ӳɱ���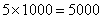 ��Ԫ����
��Ԫ����
ӡ��˰��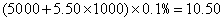 ��Ԫ����
��Ԫ����
�����ѣ�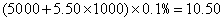 ��Ԫ����
��Ԫ����
Ӷ�� ��Ԫ����
��Ԫ����
 ��
�� Ӷ��Ϊ31.50Ԫ��
Ӷ��Ϊ31.50Ԫ��
��֧���� ��Ԫ����
��Ԫ����
�����룺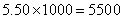 ��Ԫ����
��Ԫ����
������ν���ӯ����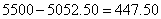 ��Ԫ����
��Ԫ����
���⣺
��1��С���Դ˺ܸ���Ȥ����ÿ��5.00Ԫ�ļ۸��������Ϲ�Ʊ100�ɣ���ÿ��5.50Ԫ�ļ۸�ȫ������������ӯ��Ϊ Ԫ��
��2��С����ÿ�� Ԫ�ļ۸��������Ϲ�Ʊ1000�ɣ����в����������ڲ�����ӯʱ�����������������������ļ۸�ÿ���� Ԫ����
Ԫ�ļ۸��������Ϲ�Ʊ1000�ɣ����в����������ڲ�����ӯʱ�����������������������ļ۸�ÿ���� Ԫ����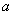 �Ĵ���ʽ��ʾ�����ɴ˿ɵ������۸�������۸��������Ҫ����
�Ĵ���ʽ��ʾ�����ɴ˿ɵ������۸�������۸��������Ҫ����  �Ų������������������Ч���֣���
�Ų������������������Ч���֣���
��3��С������ÿ��5.00Ԫ�ļ۸��������Ϲ�Ʊ1000�ɣ���ӯ��1000Ԫʱ������������������������ļ۸�ÿ���Ƕ���Ԫ������ȷ��0.01Ԫ��

![]() �ɵĹ�Ʊ����Ϊ�������ɱ��Ҫ���ɣ�
�ɵĹ�Ʊ����Ϊ�������ɱ��Ҫ���ɣ�![]() ���㣻
���㣻![]() ���㣻
���㣻![]() ���㣨���ⰴ
���㣨���ⰴ![]() ���㣩������5Ԫ��5Ԫ���㣮
���㣩������5Ԫ��5Ԫ���㣮![]() ���������Ʊ����������1000�ɣ���ÿ��5.50Ԫ�ļ۸�ȫ����������ӯ�����٣�
���������Ʊ����������1000�ɣ���ÿ��5.50Ԫ�ļ۸�ȫ����������ӯ�����٣�![]() ��Ԫ����
��Ԫ����![]() ��Ԫ����
��Ԫ����![]() ��Ԫ����
��Ԫ����![]() ��Ԫ����
��Ԫ����![]() ��
��![]() Ӷ��Ϊ31.50Ԫ��
Ӷ��Ϊ31.50Ԫ��![]() ��Ԫ����
��Ԫ����![]() ��Ԫ����
��Ԫ����![]() ��Ԫ����
��Ԫ����![]() Ԫ�ļ۸��������Ϲ�Ʊ1000�ɣ����в����������ڲ�����ӯʱ�����������������������ļ۸�ÿ���� Ԫ����
Ԫ�ļ۸��������Ϲ�Ʊ1000�ɣ����в����������ڲ�����ӯʱ�����������������������ļ۸�ÿ���� Ԫ����![]() �Ĵ���ʽ��ʾ�����ɴ˿ɵ������۸�������۸��������Ҫ����
�Ĵ���ʽ��ʾ�����ɴ˿ɵ������۸�������۸��������Ҫ���� ![]() �Ų������������������Ч���֣���
�Ų������������������Ч���֣��� �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
 ԭ�㣬�뾶Ϊr��Բ�ķ��̣�
ԭ�㣬�뾶Ϊr��Բ�ķ��̣�



