
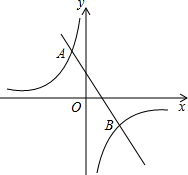
 如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$d的图象都经过点A(-2,6)和点B(4,n).
如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$d的图象都经过点A(-2,6)和点B(4,n).分析 (1)将点A(-2,6)代入y=$\frac{m}{x}$于是得到反比例函数的解析式为y=$\frac{-12}{x}$,将B(4,n)代入y=-$\frac{12}{x}$求得B(4,-3),将A,B代入y=kx+b得解方程组即可得到;
(2)设直线AB交x轴于N,交y轴于M,则M(0,3),N(2,0)
求得点N关于y轴的对称点N′(-2,0),解方程组即可得到结论;
(3)令$\frac{3}{2}$x-3=-$\frac{12}{x}$,化简得x2+2x+8=0,由于△=22-32<0,得到直线l与反比例函数y=$\frac{m}{x}$的图象无交点,设将直线l向上平移m个单位后,正好与反比例函数的图象有一个交点,则$\frac{3}{2}$x+3+m=-$\frac{12}{x}$有唯一解解方程得到m=-3+6$\sqrt{2}$,即可得到结论.
解答 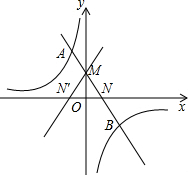 解:(1)将点A(-2,6)代入y=$\frac{m}{x}$得m=-12,
解:(1)将点A(-2,6)代入y=$\frac{m}{x}$得m=-12,
∴反比例函数的解析式为y=$\frac{-12}{x}$,
将B(4,n)代入y=-$\frac{12}{x}$得n=-3,
∴B(4,-3),
将A,B代入y=kx+b得$\left\{\begin{array}{l}{6=-2k+b}\\{-3=4k+b}\end{array}\right.$,
∴$\left\{\begin{array}{l}{k=-\frac{3}{2}}\\{b=3}\end{array}\right.$,
∴一次函数的解析式为y=-$\frac{3}{2}$x+3;
(2)如图,设直线AB交x轴于N,交y轴于M,则M(0,3),N(2,0)
∴点N关于y轴的对称点N′(-2,0),直线l过M,N′两点,
设直线l的解析式为y=k1x+b1,
∴$\left\{\begin{array}{l}{{b}_{1}=3}\\{-2{k}_{1}+{b}_{1}=0}\\{\;}\end{array}\right.$,
∴$\left\{\begin{array}{l}{{k}_{1}=\frac{3}{2}}\\{{b}_{1}=3}\end{array}\right.$,
∴直线l的解析式为y=$\frac{3}{2}$x+3;
(3)令$\frac{3}{2}$x-3=-$\frac{12}{x}$,化简得x2+2x+8=0,
∴△=22-32<0,
∴方程无解,
∴直线l与反比例函数y=$\frac{m}{x}$的图象无交点,
设将直线l向上平移m个单位后,正好与反比例函数的图象有一个交点,则$\frac{3}{2}$x+3+m=-$\frac{12}{x}$有唯一解,
∴方程3x2+2(3+m)x+24=0有两个不为零的相等根,
∴△1=4(3+m)2-3×4×24=0,解得:m=-3±6$\sqrt{2}$,
∵m>0,
∴m=-3+6$\sqrt{2}$,
∴将直线l向上平移(-3+6$\sqrt{2}$)个单位,正好与反比例函数的图象有一个交点.
点评 本题考查了反比例函数与一次函数的交点问题:求反比例函数与一次函数的解析式和交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:解答题
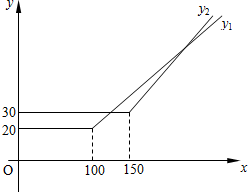 某电信公司提供的移动通讯服务的收费标准有两种套餐如表:
某电信公司提供的移动通讯服务的收费标准有两种套餐如表:| A套餐 | B套餐 | |
| 每月基本服务费 | a | 30 |
| 每月免费通话时间 | 100 | b |
| 超出每分钟收费 | 0.4 | 0.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
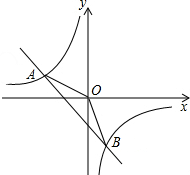 如图所示,一次函数y1=kx+b的图象与反比例函数y2=$\frac{m}{x}$的图象交于A(-2,n),B(1,-3)两点.
如图所示,一次函数y1=kx+b的图象与反比例函数y2=$\frac{m}{x}$的图象交于A(-2,n),B(1,-3)两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知直线y=kx+b与x轴、y轴分别交于A、B两点,与反比例函数交于一象限内的P($\frac{1}{2}$,n),Q(4,m)两点,且tan∠BOP=$\frac{1}{16}$:
已知直线y=kx+b与x轴、y轴分别交于A、B两点,与反比例函数交于一象限内的P($\frac{1}{2}$,n),Q(4,m)两点,且tan∠BOP=$\frac{1}{16}$:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 同位角相等 | |
| B. | 三角形的三个内角中,至少有一个不大于60° | |
| C. | 任何数的零次幂都是1 | |
| D. | 垂直于同一直线的两条直线互相垂直 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com