
【题目】如图,BD是△ABC的角平分线,它的垂直平分线分别交AB,BD,BC于点E,F,G,连接ED,DG.
(1)请判断四边形EBGD的形状,并说明理由;
(2)若∠ABC=30°,∠C=45°,ED=2![]() ,点H是BD上的一个动点,求HG+HC的最小值.
,点H是BD上的一个动点,求HG+HC的最小值.

【答案】(1)四边形EBGD是菱形,理由见解析;(2)![]() .
.
【解析】试题分析:(1)四边形EBGD是菱形,根据已知条件易证△EFD≌△GFB,可得ED=BG,所以BE=ED=DG=GB,即可判定四边形EBGD是菱形.(2)作EM⊥BC于M,DN⊥BC于N,连接EC交BD于点H,此时HG+HC最小,在RT△EMC中,求出EM、MC即可解决问题.
试题解析:(1)四边形EBGD是菱形.
理由:∵EG垂直平分BD,
∴EB=ED,GB=GD,
∴∠EBD=∠EDB,
∵∠EBD=∠DBC,
∴∠EDF=∠GBF,
在△EFD和△GFB中,
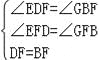 ,
,
∴△EFD≌△GFB,
∴ED=BG,
∴BE=ED=DG=GB,
∴四边形EBGD是菱形.
(2)作EM⊥BC于M,DN⊥BC于N,连接EC交BD于点H,此时HG+HC最小,
在RT△EBM中,∵∠EMB=90°,∠EBM=30°,EB=ED=2![]() ,
,
∴EM=![]() BE=
BE=![]() ,
,
∵DE∥BC,EM⊥BC,DN⊥BC,
∴EM∥DN,EM=DN=![]() ,MN=DE=2
,MN=DE=2![]() ,
,
在RT△DNC中,∵∠DNC=90°,∠DCN=45°,
∴∠NDC=∠NCD=45°,
∴DN=NC=![]() ,
,
∴MC=3![]() ,
,
在RT△EMC中,∵∠EMC=90°,EM=![]() .MC=3
.MC=3![]() ,
,
∴EC=![]() =
=![]() =10.
=10.
∵HG+HC=EH+HC=EC,
∴HG+HC的最小值为10.



 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
【题目】下列事件中,必然事件是( )
A.抛掷1个均匀的骰子,出现6点向上
B.两直线被第三条直线所截,同位角相等
C.366人中至少有2人的生日相同
D.实数的绝对值是非负数
查看答案和解析>>
科目:初中数学 来源: 题型:
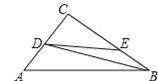
【题目】如图,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点D从点C出发,以2cm/s的速度沿折线C﹣A﹣B向点B运动,同时,点E从点B出发,以1cm/s的速度沿BC边向点C运动,设点E运动的时间为t(s)(0<t<8).
(1)求AB的长;
(2)当△BDE是直角三角形时,求t的值;
(3)设△CDE的面积为y(cm2),求y与t的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班数学学习小组某次测验成绩分别是63,72,70,49,66,81,53,92,69,则这组数据的极差是( )
A. 47 B. 43 C. 34 D. 29
查看答案和解析>>
科目:初中数学 来源: 题型:
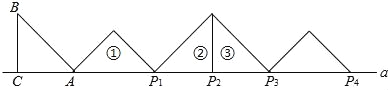
【题目】如图,等腰Rt△ABC中,∠ACB=90°,AC=BC=1,且AC边在直线a上,将△ABC绕点A顺时针旋转到位置①可得到点P1,此时AP1=![]() ;将位置①的三角形绕点P1顺时针旋转到位置②可得到点P2,此时AP2=
;将位置①的三角形绕点P1顺时针旋转到位置②可得到点P2,此时AP2=![]() +1;将位置②的三角形绕点P2顺时针旋转到位置③可得到点P3时,AP3=
+1;将位置②的三角形绕点P2顺时针旋转到位置③可得到点P3时,AP3=![]() +2…按此规律继续旋转,直至得到点P2026为止,则AP2016= .
+2…按此规律继续旋转,直至得到点P2026为止,则AP2016= .
查看答案和解析>>
科目:初中数学 来源: 题型:
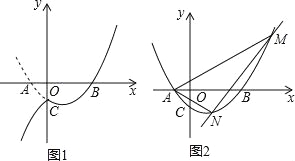
【题目】已知抛物线y=(m﹣1)x2+(m﹣2)x﹣1与x轴交于A、B两点,若m>1,且点A在点B的左侧,OA:OB=1:3
(1)试确定抛物线的解析式;
(2)直线y=kx﹣3与抛物线交于M、N两点,若△AMN的内心在x轴上,求k的值.
(3)设(2)中抛物线与y轴的交点为C,过点C作直线l∥x轴,将抛物线在y轴左侧的部分沿直线l翻折,抛物线的其余部分保持不变,得到一个新图象,请你结合新图象回答:当直线y=![]() x+b与新图象只有一个公共点P(x0,y0)且y0≤7时,求b的取值范围.
x+b与新图象只有一个公共点P(x0,y0)且y0≤7时,求b的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com