
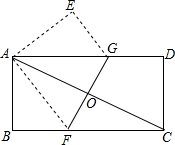
 如图,将一矩形纸片ABCD折叠,使两个顶点A,C重合,折痕为FG..若AB=8,BC=16,则△AEG的面积为24.
如图,将一矩形纸片ABCD折叠,使两个顶点A,C重合,折痕为FG..若AB=8,BC=16,则△AEG的面积为24. 科目:初中数学 来源: 题型:选择题
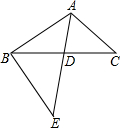 如图,△ABC中,AE交BC于点D,∠C=∠E,AD=4,BC=8,BD:DC=5:3,则DE的长等于( )
如图,△ABC中,AE交BC于点D,∠C=∠E,AD=4,BC=8,BD:DC=5:3,则DE的长等于( )| A. | $\frac{20}{3}$ | B. | $\frac{17}{4}$ | C. | $\frac{16}{3}$ | D. | $\frac{15}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在边长为2的正方形ABCD中,G是AD延长线上的一点,且DG=AD,动点M从A点出发,以每秒1个单位的速度沿着A→C→G的路线向G点匀速运动(M不与A,G重合),设运动时间为t秒,连接BM并延长交AG于N.
如图,在边长为2的正方形ABCD中,G是AD延长线上的一点,且DG=AD,动点M从A点出发,以每秒1个单位的速度沿着A→C→G的路线向G点匀速运动(M不与A,G重合),设运动时间为t秒,连接BM并延长交AG于N.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某型号飞机的机翼形状如图所示,AB∥CD,∠DAE=37°,∠CBE=45°,CD=1.4m,AB、CD之间的距离为5.1m.求AD、AB的长.
某型号飞机的机翼形状如图所示,AB∥CD,∠DAE=37°,∠CBE=45°,CD=1.4m,AB、CD之间的距离为5.1m.求AD、AB的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
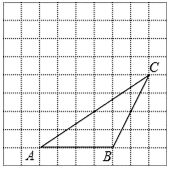 如图,△ABC的顶点都在方格纸的格点上.将△ABC向左平移2格,再向上平移4格.请在图中画出平移后的△A′B′C′,再在图中画出△A′B′C′的高C′D′、中线A′E,若S△BCP=S△ACB,P为异于点B的格点,则点P的个数为4个.
如图,△ABC的顶点都在方格纸的格点上.将△ABC向左平移2格,再向上平移4格.请在图中画出平移后的△A′B′C′,再在图中画出△A′B′C′的高C′D′、中线A′E,若S△BCP=S△ACB,P为异于点B的格点,则点P的个数为4个.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
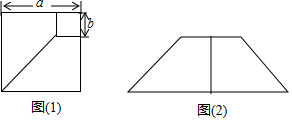
| A. | (a+b)2=a2+2ab+b2 | B. | (a-b)2=a2-2ab+b2 | C. | a2-b2=(a+b)(a-b) | D. | (a+b)2-(a-b)2=4ab |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com