
【题目】点![]() 是
是![]() 内一点,且点
内一点,且点![]() 到三边的距离相等,
到三边的距离相等,![]() ,则
,则![]() ________.
________.
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
【题目】两块等腰直角三角板△ABC和△DEC如图摆放,其中∠ACB=∠DCE=90°,F是DE的中点,H是AE的中点,G是BD的中点.
(1)如图1,若点D、E分别在AC、BC的延长线上,通过观察和测量,猜想FH和FG的数量关系为______和位置关系为______;
(2)如图2,若将三角板△DEC绕着点C顺时针旋转至ACE在一条直线上时,其余条件均不变,则(1)中的猜想是否还成立,若成立,请证明,不成立请说明理由;
(3)如图3,将图1中的△DEC绕点C顺时针旋转一个锐角,得到图3,(1)中的猜想还成立吗?直接写出结论,不用证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,已知点P0的坐标为(![]() ,
,![]() ),将线段OP0按逆时针方向旋转45°,再将其长度伸长为OP0的2倍,得到线段OP1;又将线段OP1按逆时针方向旋转45°,长度伸长为OP1的2倍,得到线段OP2;如此下去,得到线段OP3,OP4,…,OPn(n为正整数),则点P2017的坐标为( )
),将线段OP0按逆时针方向旋转45°,再将其长度伸长为OP0的2倍,得到线段OP1;又将线段OP1按逆时针方向旋转45°,长度伸长为OP1的2倍,得到线段OP2;如此下去,得到线段OP3,OP4,…,OPn(n为正整数),则点P2017的坐标为( )

A. (![]() ,
,![]() ) B. (0,22018) C. (
) B. (0,22018) C. (![]() ,
,![]() ) D. (22018,0)
) D. (22018,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系内,点O为坐标原点,点A在x轴负半轴上,点B、C分别在x轴、y轴正半轴上,且OB=2OA,OBOC=OCOA=2.
(1)求点C的坐标;
(2)点P从点A出发以每秒1个单位的速度沿AB向点B匀速运动,同时点Q从点B出发以每秒3个单位的速度沿BA向终点A匀速运动,当点Q到达终点A时,点P、Q均停止运动,设点P运动的时间为t(t>0)秒,线段PQ的长度为y,用含t的式子表示y,并写出相应的t的范围;
(3)在(2)的条件下,过点P作x轴的垂线PM,PM=PQ,是否存在t值使点O为PQ中点? 若存在求t值并求出此时△CMQ的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形ABCD,点P为BC边上一动点,连接AP,将线段AP绕P点顺时针旋转90°,点A恰好落在直线CD上点E处.
(1)如图1,点E在线段CD上,求证:AD+DE=2AB;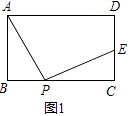
(2)如图2,点E在线段CD的延长线上,且点D为线段CE的中点,在线段BD上取点F,连接AF、PF,若AF=AB.求证:∠APF=∠ADB.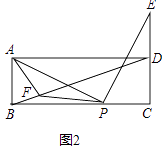
(3)如图3,点E在线段CD上,连接BD,若AB=2,BD∥PE,则DE= . (直接写出结果)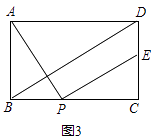
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在甲、乙两名同学中选拔一人参加“中华好诗词”大赛,在相同的测试条件下,两人5次测试成绩(单位:分)如下:
甲:79,86,82,85,83
乙:88,79,90,81,72.
回答下列问题:
(1)甲成绩的平均数是______ ,乙成绩的平均数是______ ;
(2)经计算知S甲2=6,S乙2=42.你认为选拔谁参加比赛更合适,说明理由;
(3)如果从甲、乙两人5次的成绩中各随机抽取一次成绩进行分析,求抽到的两个人的成绩都大于80分的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com