
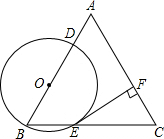
 (2013•滨州)如图,在△ABC中,AB=AC,点O在边AB上,⊙O过点B且分别与边AB、BC相交于点D、E,EF⊥AC,垂足为F.求证:直线EF是⊙O的切线.
(2013•滨州)如图,在△ABC中,AB=AC,点O在边AB上,⊙O过点B且分别与边AB、BC相交于点D、E,EF⊥AC,垂足为F.求证:直线EF是⊙O的切线.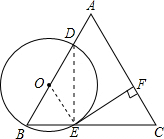 解:方法一:
解:方法一: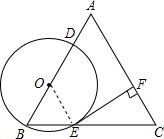


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
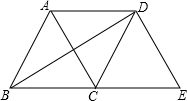 (2013•滨州)如图,等边△ABC沿射线BC向右平移到△DCE的位置,连接AD、BD,则下列结论:
(2013•滨州)如图,等边△ABC沿射线BC向右平移到△DCE的位置,连接AD、BD,则下列结论:查看答案和解析>>
科目:初中数学 来源: 题型:
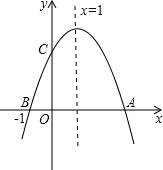 (2013•滨州)如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,且对称轴为x=1,点B坐标为(-1,0).则下面的四个结论:
(2013•滨州)如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,且对称轴为x=1,点B坐标为(-1,0).则下面的四个结论:查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•滨州)某高中学校为高一新生设计的学生板凳的正面视图如图所示,其中BA=CD,BC=20cm,BC、EF平行于地面AD且到地面AD的距离分别为40cm、8cm.为使板凳两腿底端A、D之间的距离为50cm,那么横梁EF应为多长?(材质及其厚度等暂忽略不计).
(2013•滨州)某高中学校为高一新生设计的学生板凳的正面视图如图所示,其中BA=CD,BC=20cm,BC、EF平行于地面AD且到地面AD的距离分别为40cm、8cm.为使板凳两腿底端A、D之间的距离为50cm,那么横梁EF应为多长?(材质及其厚度等暂忽略不计).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com