
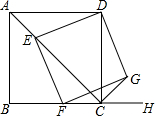
 如图,已知四边形ABCD为正方形,AB=$2\sqrt{2}$,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE.交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.
如图,已知四边形ABCD为正方形,AB=$2\sqrt{2}$,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE.交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.分析 (1)作出辅助线,得到EN=EM,然后判断∠DEN=∠FEM,得到△DEN≌△FEM,则有DE=EF即可;
(2)同(1)的方法证出△ADE≌△CDG得到CG=AE,得出CE+CG=CE+AE=AC=4即可.
解答 ①证明:过E作EM⊥BC于M点,过E作EN⊥CD于N点,如图所示: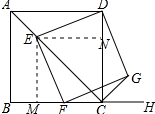
∵正方形ABCD
∴∠BCD=90°,∠ECN=45°
∴∠EMC=∠ENC=∠BCD=90°
且NE=NC,
∴四边形EMCN为正方形
∵四边形DEFG是矩形,
∴EM=EN,∠DEN+∠NEF=∠MEF+∠NEF=90°
∴∠DEN=∠MEF,
又∠DNE=∠FME=90°,
在△DEN和△FEM中,$\left\{\begin{array}{l}{∠DNE=∠FME}&{\;}\\{EN=EM}&{\;}\\{∠DEN=∠FEM}&{\;}\end{array}\right.$,
∴△DEN≌△FEM(ASA),
∴ED=EF,
∴矩形DEFG为正方形,
②解:CE+CG的值为定值,理由如下:
∵矩形DEFG为正方形,
∴DE=DG,∠EDC+∠CDG=90°
∵四边形ABCD是正方形,
∵AD=DC,∠ADE+∠EDC=90°
∴∠ADE=∠CDG,
在△ADE和△CDG中,$\left\{\begin{array}{l}{AD=CD}&{\;}\\{∠ADE=∠CDG}&{\;}\\{DE=DG}&{\;}\end{array}\right.$,
∴△ADE≌△CDG(SAS),
∴AE=CG
∴AC=AE+CE=$\sqrt{2}$AB=$\sqrt{2}$×2$\sqrt{2}$=4,
∴CE+CG=4 是定值.
点评 此题是四边形综合题,主要考查了正方形的性质,矩形的性质,矩形的判定,三角形的全等的性质和判定,勾股定理,解本题的关键是作出辅助线,判断三角形全等.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:解答题
 某粮油超市平时每天都将一定数量的某些品种的粮食进行包装以便出售,已知每天包装大黄米的质量是包装江米质量$\frac{5}{4}$倍,且每天包装大黄米和江米的质量之和为45千克.
某粮油超市平时每天都将一定数量的某些品种的粮食进行包装以便出售,已知每天包装大黄米的质量是包装江米质量$\frac{5}{4}$倍,且每天包装大黄米和江米的质量之和为45千克.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 销售方式 | 粗加工后销售 | 精加工后销售 |
| 每吨获利(元) | 1000 | 2000 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 恩 | B. | 施 | C. | 城 | D. | 同 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某企业车间有技术工人20人,车间为了合理制定产品的每月生产定额,作了这20人某月加工零件个数的条形统计图.
某企业车间有技术工人20人,车间为了合理制定产品的每月生产定额,作了这20人某月加工零件个数的条形统计图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com