
【题目】如图,边长为2的正方形ABCD的顶点A在y轴上,顶点D在反比例函数y= ![]() (x>0)的图象上,已知点B的坐标是(
(x>0)的图象上,已知点B的坐标是( ![]() ,
, ![]() ),则k的值为( )
),则k的值为( )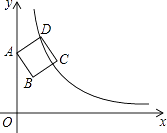
A.4
B.6
C.8
D.10
【答案】C
【解析】如图,过点B作BE⊥y轴于E,过点D作DF⊥y轴于F,
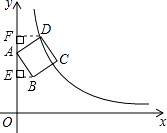
在正方形ABCD中,AB=AD,∠BAD=90°,
∴∠BAE+∠DAF=90°,
∵∠DAF+∠ADF=90°,
∴∠BAE=∠ADF,
在△ABE和△DAF中,
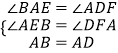 ,
,
∴△ABE≌△DAF(AAS),
∴AF=BE,DF=AE,
∵正方形的边长为2,B( ![]() ,
, ![]() ),
),
∴BE= ![]() ,AE=
,AE= ![]() =
= ![]() ,
,
∴OF=OE+AE+AF= ![]() +
+ ![]() +
+ ![]() =5,
=5,
∴点D的坐标为( ![]() ,5),
,5),
∵顶点D在反比例函数y= ![]() (x>0)的图象上,
(x>0)的图象上,
∴k=xy= ![]() ×5=8.
×5=8.
所以答案是:C.
【考点精析】通过灵活运用正方形的性质,掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形即可以解答此题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】已知第三象限的点P(x,y)满足![]() ,
,![]() .
.
(1)求点P的坐标;
(2)①点P到x轴的距离为_______;
②把点P向右平移m个单位后得到P1,则点P1到x轴的距离为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一个边长为![]() 的正方形图形分割成四部分,观察图形,解答下列问题:
的正方形图形分割成四部分,观察图形,解答下列问题:
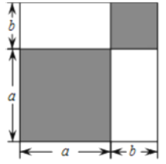
(1)根据图中条件,请用两种方法表示该阴影图形的总面积
方法1:_________________方法2__________________;
由此可得等量关系:______________________________;
应用该等量关系解决下列问题:
(2)若图中的a,b(![]() )满足
)满足![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知△ABC的三个顶点的坐标分别为A(﹣2,3),B(﹣6,0),C(﹣1,0).
(1)请直接写出点B关于点A对称的点的坐标;
(2)将△ABC绕坐标原点O逆时针旋转90°,画出图形,直接写出点B的对应点的坐标;
(3)请直接写出:以A,B,C为顶点的平行四边形的第四个顶点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,![]() ,E是边CD的中点,连接BE并延长与AD的延长线相较于点F.若△BCD是等腰三角形,则四边形BDFC的面积为_______________。
,E是边CD的中点,连接BE并延长与AD的延长线相较于点F.若△BCD是等腰三角形,则四边形BDFC的面积为_______________。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了抗击新冠病毒,保护学生和教师的生命安全,新希望中学![]() 元购进甲、乙两种医用口罩共计
元购进甲、乙两种医用口罩共计![]() 盒,甲,乙两种口罩的售价分别是
盒,甲,乙两种口罩的售价分别是![]() 元/盒,
元/盒,![]() 元/盒;甲,乙两 种口罩的数量分别是
元/盒;甲,乙两 种口罩的数量分别是![]() 个/盒,
个/盒,![]() 个/盒.
个/盒.
(1)求新希望中学甲、乙两种口罩各购进了多少盒?
(2)按照教育局要求,学校必须储备两周的用量,新希望中学师生共计![]() 人,每人每天
人,每人每天![]() 个口罩,问购买的口罩数量是否能满足教育局的要求?
个口罩,问购买的口罩数量是否能满足教育局的要求?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在Rt△ABC中,∠B=30°,∠ACB=90°,延长CA到O,使AO=AC,以O为圆心,OA长为半径作⊙O交BA延长线于点D,连接CD.
(1)求证:CD是⊙O的切线;
(2)若AB=4,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标xOy中,正比例函数y=kx的图象与反比例函数y= ![]() 的图象都经过点A(2,﹣2).
的图象都经过点A(2,﹣2).
(1)分别求这两个函数的表达式;
(2)将直线OA向上平移3个单位长度后与y轴交于点B,与反比例函数图象在第四象限内的交点为C,连接AB,AC,求点C的坐标及△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com