
【题目】推理填空
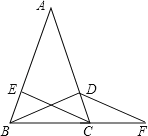
如图:∠ABC=∠ACB,BD平分∠ABC,CE平分∠ACB,∠DBF=∠F,求证:CE∥DF.请完成下面的解题过程.

解:∵BD平分∠ABC,CE平分∠ACB ( 已知 )
∴∠DBC=![]() ∠_____,∠ECB=
∠_____,∠ECB=![]() ∠_____ ( 角平分线的定义)
∠_____ ( 角平分线的定义)
又∵∠ABC=∠ACB (已知)
∴∠_____=∠_____.
又∵∠_____=∠_____ (已知)
∴∠F=∠_____
∴CE∥DF_____.
【答案】∠ABC ∠ACB ∠DBC ∠ECB ∠DBF ∠F ∠ECB 同位角相等,两直线平行
【解析】
结合角平分线的定义以及∠ABC=∠ACB即可得出∠DBC=∠ECB,再由∠DBF=∠F即可得出∠F=∠ECB,利用(同位角相等,两直线平行)即可得出CE∥DF.
∵BD平分∠ABC,CE平分∠ACB ( 已知 ),
∴∠DBC=![]() ∠ABC,∠ECB=
∠ABC,∠ECB=![]() ∠ACB( 角平分线的定义).
∠ACB( 角平分线的定义).
又∵∠ABC=∠ACB (已知),
∴∠DBC=∠ECB.
又∵∠DBF=∠F(已知),
∴∠F=∠ECB(等量代换),
∴CE∥DF(同位角相等,两直线平行).
故答案为:ABC;ACB;DBC;ECB;DBF;F;ECB;同位角相等,两直线平行.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】一个口袋中放有290个涂有红、黑、白三种颜色的质地相同的小球.若红球个数是黑球个数的2倍多40个.从袋中任取一个球是白球的概率是![]() .
.
(1)求袋中红球的个数;
(2)求从袋中任取一个球是黑球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=![]() x+3与x轴交于点A,与y轴交于点B,点C与点A关于y轴对称.
x+3与x轴交于点A,与y轴交于点B,点C与点A关于y轴对称.
(1)求直线BC的函数表达式;
(2)设点M是x轴上的一个动点,过点M作y轴的平行线,交直线AB于点P,交直线BC于点Q,连接BM.
①若∠MBC=90°,求点P的坐标;
②若△PQB的面积为![]() ,请直接写出点M的坐标.
,请直接写出点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 问题解决:
问题解决:![]() 如图1,在平面直角坐标系xOy中,一次函数
如图1,在平面直角坐标系xOy中,一次函数![]() 与x轴交于点A,与y轴交于点B,以AB为腰在第二象限作等腰直角
与x轴交于点A,与y轴交于点B,以AB为腰在第二象限作等腰直角![]() ,
,![]() ,点A、B的坐标分别为A______、B______.
,点A、B的坐标分别为A______、B______.
![]() 求
求![]() 中点C的坐标.小明同学为了解决这个问题,提出了以下想法:过点C向x轴作垂线交x轴于点
中点C的坐标.小明同学为了解决这个问题,提出了以下想法:过点C向x轴作垂线交x轴于点![]() 请你借助小明的思路,求出点C的坐标;
请你借助小明的思路,求出点C的坐标;
![]() 类比探究:数学老师表扬了小明同学的方法,然后提出了一个新的问题,如图2,在平面直角坐标系xOy中,点A坐标
类比探究:数学老师表扬了小明同学的方法,然后提出了一个新的问题,如图2,在平面直角坐标系xOy中,点A坐标![]() ,点B坐标
,点B坐标![]() ,过点B作x轴垂线l,点P是l上一动点,点D是在一次函数
,过点B作x轴垂线l,点P是l上一动点,点D是在一次函数![]() 图象上一动点,若
图象上一动点,若![]() 是以点D为直角顶点的等腰直角三角形,请直接写出点D与点P的坐标.
是以点D为直角顶点的等腰直角三角形,请直接写出点D与点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王老师在公园道一号购买了一套经济适用房,他准备将地面铺上地砖,地面结构如图所示,根据图中的数据(单位:m),解答下列问题:

(1)用含x的代数式表示地面总面积
(2)当x=3时,若铺1m2地砖的平均费用为100元, 那么王老师要将全部地面铺地砖,总费用为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某市市民晚饭后1小时内的生活方式,调查小组设计了“阅读”、“锻炼”、“看电视”和“其它”四个选项,用随机抽样的方法调查了该市部分市民,并根据调查结果绘制成如下统计图.根据统计图所提供的信息,解答下列问题:
(1)本次共调查了名市民;
(2)补全条形统计图;并在条形图上方写上数据;
(3)该市共有480万市民,估计该市市民晚饭后1小时内锻炼的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一盛有部分水的圆柱形小水杯放入事先没有水的大圆柱形容器内,现用一注水管沿大容器内壁匀速注水(如图所示),则小水杯内水面的高度h(cm)与注水时间t(min)的函数图象大致为( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明:
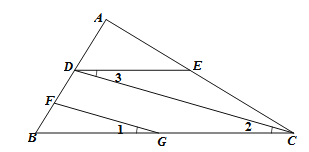
如图,FG//CD,∠1=∠3,∠B=50°,求∠BDE的度数.
解:∵FG//CD (已知)
∴∠2=_________( )
又∵∠1=∠3
∴∠3=∠_________( )
∴BC//__________( )
∴∠B+________=180°( )
又∵∠B=50°
∴∠BDE=130°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上有A. B.C三点,分别表示有理数26,10,10,动点P从A出发,以每秒1个单位的速度向终点C移动,设点P移动时间为t秒。
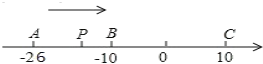
(1)PA= ,PC= (用含t的代数式表示)
(2)当点P运动到B点时,点Q从A点出发,以每秒3个单位的速度向C点运动,Q点到达C点后,再立即以同样的速度返回,当点P运动到点C时,P、Q两点运动停止,
①当P、Q两点运动停止时,求点P和点Q的距离;
②求当t为何值时P、Q两点恰好在途中相遇.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com