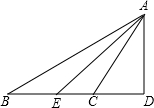
三角形内角和定理 ∠BAC 34°

90° 三角形外角的性质 ∠CAE 37°
分析:先由三角形内角和定理得出∠B+∠ACB+∠BAC=180°的度数,故可得出∠BAC的度数,根据AE是∠BAC的平分线可求出∠CAE的度数,再由AD是BC边上的高 即AD⊥BC可知∠D的度数,再由∠ACE是△ACD的外角可知∠ACE=∠CAD+∠D,故可得出∠CAD的度数,进而得出∠DAE的度数.
解答:在ABC中,
∵∠B+∠ACB+∠BAC=180°(三角形内角和定理)
∴∠BAC=180°-∠B-∠BAC(等式的性质)
=180°-36°-110°=34°
∵AE是∠BAC的平分线(已知)
∴∠CAE=

∠BAC=17°
∵AD是BC边上的高 即AD⊥BC (已知)
∴∠D=90°,
∵∠AC E是△ACD的外角 (已知)
∴∠ACE=∠CAD+∠D(三角形外角的性质)
∴∠CAD=∠ACE-∠D (等式的性质)
=110°-90°=20°
∴∠DAE=∠CAD+∠CAE
=20°+17°
=37°.
故答案为:三角形内角和定理;∠BAC;34°;

;90°;三角形外角的性质;∠CAE;37°.
点评:本题考查的是三角形内角和定理及三角形外角的性质,熟知三角形的内角和是180°是解答此题的关键.

 说理解答题
说理解答题 90° 三角形外角的性质 ∠CAE 37°
90° 三角形外角的性质 ∠CAE 37° ∠BAC=17°
∠BAC=17° ;90°;三角形外角的性质;∠CAE;37°.
;90°;三角形外角的性质;∠CAE;37°.

 字词句段篇系列答案
字词句段篇系列答案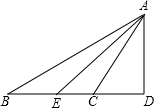 说理解答题
说理解答题