
分析 将$\sqrt{ab}$,$\sqrt{bc}$,$\sqrt{ac}$分别转化为相同的分子,然后通过比较分母的大小得到$\sqrt{ab}$,$\sqrt{bc}$,$\sqrt{ac}$的大小顺序.
解答 解:$\sqrt{ab}$=$\sqrt{\frac{abc}{c}}$,$\sqrt{bc}$=$\sqrt{\frac{abc}{a}}$,$\sqrt{ac}$=$\sqrt{\frac{abc}{b}}$,
∵0<c<b<a,
∴$\sqrt{\frac{abc}{c}}$>$\sqrt{\frac{abc}{b}}$>$\sqrt{\frac{abc}{a}}$,
∴$\sqrt{{c}^{2}}$<$\sqrt{bc}$<$\sqrt{ac}$<$\sqrt{bc}$,即c<$\sqrt{bc}$<$\sqrt{ac}$<$\sqrt{bc}$,
故答案是:c<$\sqrt{bc}$<$\sqrt{ac}$<$\sqrt{bc}$.
点评 本题考查了实数大小比较.注意两个无理数的比较方法:统一根据二次根式的性质,把根号外的移到根号内,只需比较被开方数的大小.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
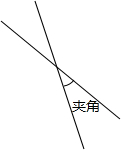 两条直线相交,四个交角中的一个锐角或一个直角称为这两条直线的”夹角”(见图3).如果在平面上画L条直线,要求它们两两相交,并且”夹角”只能是15°,30°,45°,60°,75°,90°之一,问:
两条直线相交,四个交角中的一个锐角或一个直角称为这两条直线的”夹角”(见图3).如果在平面上画L条直线,要求它们两两相交,并且”夹角”只能是15°,30°,45°,60°,75°,90°之一,问:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 密码 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 对应数字 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
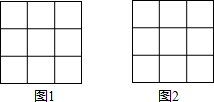 如图,在3×3的正方形网格中,每个小正方形的边长都是1,每个小格的顶点叫格点,以格点为顶点,分别按下列要求画三角形:
如图,在3×3的正方形网格中,每个小正方形的边长都是1,每个小格的顶点叫格点,以格点为顶点,分别按下列要求画三角形:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com