
【题目】如图,已知抛物线经过点A(2,0)和B(t,0)(t≥2),与y轴交于点C,直线l:y=x+2t经过点C,交x轴于点D,直线AE交抛物线于点E,且有∠CAE=∠CDO,作CF⊥AE于点F.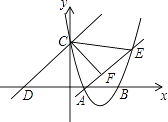
(1)求∠CDO的度数;
(2)求出点F坐标的表达式(用含t的代数式表示);
(3)当S△COD﹣S四边形COAF=7时,求抛物线解析式;
(4)当以B,C,O三点为顶点的三角形与△CEF相似时,请直接写出t的值.
【答案】
(1)
解:∵直线l:y=x+2t与y轴点C,交x轴于点D,
∴C(0,2t),D(﹣2t,0)
∴OC=OD,
∵∠COD=90°,
∴∠CDO=∠DCO=45°
(2)
解:如图1,作FG⊥x轴于点G,FH⊥y轴于点H,

∵∠HOG=∠OGF=∠FHO=90°,
∴四边形OGFH是矩形
∴∠HFG=90°,
∴∠HFA+∠AFG=90°
又∵CF⊥AE,
∴∠CFH+∠HFA=90°
∴∠CFH=∠AFG,
又∵∠CAE=∠CDO=45°,
∴∠FCA=45°,
∴CF=AF,
又∵∠FGA=∠CHF=90°,
在△FGA和△FHC中,

∴△FGA≌△FHC,
∴FH=FG,HC=AG,
设F(m,m)
则2t﹣m=m﹣2,
得m=t+1,
∴F(t+1,t+1)
(3)
解:∵S△COD﹣S四边形COAF=S△COD﹣S正方形HOGF=7
∴ ![]() =7,
=7,
解得:t=4或﹣2(舍去),
则A点坐标(2,0),B点坐标(4,0),C点坐标(0,8)
设y=a(x﹣2)(x﹣4),
把C(0,8)代入y=a(x﹣2)(x﹣4),
解得a=1,
∴y=(x﹣2)(x﹣4)=x2﹣6x+8
(4)
解:t=3或2.
如图2,作ET⊥HF于T,

求得:E的横坐标是 ![]() ,CH=t﹣1,FT=
,CH=t﹣1,FT= ![]() ,
,
由△HCF∽△TFE,
则 ![]() ,
,
得: ![]()
当△OBC∽△FEC时, ![]() =2,
=2,
即 ![]() =2,
=2,
解得:t=3或t=﹣1( 舍去),
当△OBC∽△FCE时, ![]() ,
,
即 ![]() ,
,
解得:t=2或t=0(舍去).
∴t=3或2
【解析】(1)求出点C,D的坐标,得到OC=OD,即可解答;(2)如图1,作FG⊥x轴于点G,FH⊥y轴于点H,利用已知条件证明△FGA≌△FHC,得到FH=FG,HC=AG,设F(m,m)则2t﹣m=m﹣2,求出m的值,即可解答;(3)如图2,作ET⊥HF于T,分别得到E的横坐标是 ![]() ,CH=t﹣1,FT=
,CH=t﹣1,FT= ![]() ,再由△HCF∽△TFE,得到
,再由△HCF∽△TFE,得到 ![]() ,即
,即 ![]() ,分类讨论:当△OBC∽△FEC时;当△OBC∽△FCE时;求出t的值,即可解答.
,分类讨论:当△OBC∽△FEC时;当△OBC∽△FCE时;求出t的值,即可解答.


科目:初中数学 来源: 题型:
【题目】已知:正方形纸片ABCD的边长为4,将该正方形纸片沿EF折叠(E,F分别在AB,CD边上),使点B落在AD边上的点M处,点C落在点N处,MN与CD交于点P.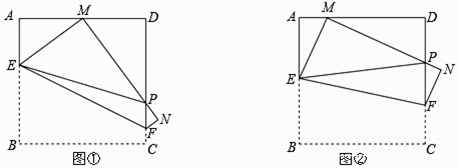
(1)如图①,连接PE,若M是AD边的中点.
①写出图中与△PMD相似的三角形.
②求△PMD的周长.
(2)如图②,随着落点M在AD边上移动(点M不与A、D重合),△PDM的周长是否发生变化?请说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的中点,过点A作AD⊥AB交BE的延长线于点D,CG平分∠ACB交BD于点G,F为AB边上一点,连接CF,且∠ACF=∠CBG.求证: 
(1)AF=CG;
(2)CF=2DE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以四边形ABCD的边AB、AD为边分别向外侧作等边三角形ABF和ADE,连接EB、FD,交点为G.
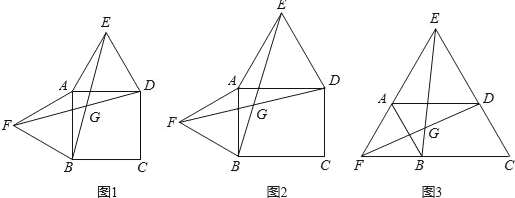
(1)当四边形ABCD为正方形时(如图1),EB和FD的数量关系是 ;
(2)当四边形ABCD为矩形时(如图2),EB和FD具有怎样的数量关系?请加以证明;
(3)四边形ABCD由正方形到矩形到一般平行四边形的变化过程中,∠EGD是否发生变化?如果改变,请说明理由;如果不变,请在图3中求出∠EGD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果两个三角形的两条边对应相等,夹角互补,那么这两个三角形叫做互补三角形,如图2,分别以△ABC的边AB、AC为边向外作正方形ABDE和ACGF,则图中的两个三角形就是互补三角形.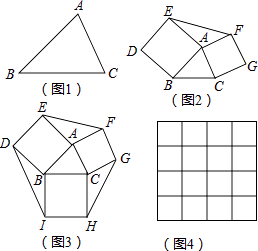
(1)图1中的△ABC的BC边上有一点D,线段AD将△ABC分成两个互补三角形,则点D在BC边的处.
(2)证明:图2中的△ABC分割成两个互补三角形面积相等;
(3)如图3,在图2的基础上再以BC为边向外作正方形BCHI,已知三个正方形面积分别是17、13、10.则图3中六边形DEFGHI的面积为 . (提示:可先利用图4求出△ABC的面积)
查看答案和解析>>
科目:初中数学 来源: 题型:
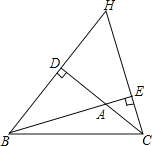
【题目】已知BD、CE是△ABC的两条高,直线BD、CE相交于点H.
(1)如图,①在图中找出与∠DBA相等的角,并说明理由;
②若∠BAC=100°,求∠DHE的度数;
(2)若△ABC中,∠A=50°,直接写出∠DHE的度数是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
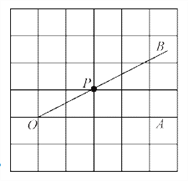
【题目】如图,在![]() 的正方形网格中,点P是
的正方形网格中,点P是![]() 的边OB上的一点.
的边OB上的一点.
(1)过点P画OB的垂线,交OA于点C;过点P画OA的垂线,垂足为H;
(2)线段PH的长度是点P到直线__________的距离;
(3)线段__________的长度是点C到直线OB的距离;
(4)线段PC、PH、OC这三条线段大小关系是__________(用“<”号连接).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)单项式﹣2x3ym与5xn+1y的差是一个单项式,求![]() 的值;
的值;
(2)化简求值:(x2+5﹣4x3)﹣2(﹣2x3+5x﹣4),其中x=﹣2;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知E、F分别为平行四边形ABCD的对边AD、BC上的点,且DE=BF,EM⊥AC于M,FN⊥AC于N,EF交AC于点O,
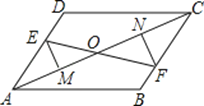
求证:(1)EM=FN;
(2)EF与MN互相平分.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com