
【题目】如图,在△ABC中,AD⊥BC于点D,点E在AB边上,连接CE,若∠BCE=2∠BAD,BE=2BD,AE:CD=3:8,S△ABC=39,则AC边的长为_____.

【答案】2![]()
【解析】
如图,在CD上截取DF=BD,由“AAS”可证△ABF≌△CBE,可得AB=BC=AF=CE,由勾股定理和三角形面积公式可求AD,CD的长,由勾股定理可求AC的长.
解:如图,在CD上截取DF=BD,
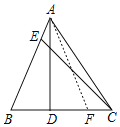
∵DF=BD,AD⊥BC,
∴AB=AF,且AD⊥BC,
∴∠BAF=2∠BAD,且∠BCE=2∠BAD,
∴∠BAF=∠BCE,且∠B=∠B,BF=2BD=BE,
∴△ABF≌△CBE(AAS)
∴AB=BC=AF=CE,
∴AE+BE=BD+CD,
∵AE:CD=3:8,
∴设AE=3x,CD=8x,
∴3x+2BD=BD+8x,
∴BD=5x,
∴AB=BC=13x,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
故答案为:2![]() .
.


科目:初中数学 来源: 题型:
【题目】在“双十一”购物街中,某儿童品牌玩具专卖店购进了![]() 两种玩具,其中
两种玩具,其中![]() 类玩具的金价比
类玩具的金价比![]() 玩具的进价每个多
玩具的进价每个多![]() 元.经调查发现:用
元.经调查发现:用![]() 元购进
元购进![]() 类玩具的数量与用
类玩具的数量与用![]() 元购进
元购进![]() 类玩具的数量相同.
类玩具的数量相同.
(1)求![]() 的进价分别是每个多少元?
的进价分别是每个多少元?
(2)该玩具店共购进![]() 了两类玩具共
了两类玩具共![]() 个,若玩具店将每个
个,若玩具店将每个![]() 类玩具定价为
类玩具定价为![]() 元出售,每个
元出售,每个![]() 类玩具定价
类玩具定价![]() 元出售,且全部售出后所获得的利润不少于
元出售,且全部售出后所获得的利润不少于![]() 元,则该淘宝专卖店至少购进
元,则该淘宝专卖店至少购进![]() 类玩具多少个?
类玩具多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点C是线段AB上一点,AC=![]() AB,BC为⊙O的直径.
AB,BC为⊙O的直径.
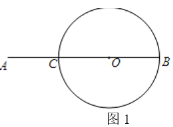
(1)在图1直径BC上方的圆弧上找一点P,使得PA=PB;(用尺规作图,保留作图痕迹,不要求写作法)
(2)连接PA,求证:PA是⊙O的切线;
(3)在(1)的条件下,连接PC、PB,∠PAB的平分线分别交PC、PB于点D、E.求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 与
与![]() 轴的两个交点是点
轴的两个交点是点![]() ,
,![]() (
(![]() 在
在![]() 的左侧),与
的左侧),与![]() 轴的交点是点
轴的交点是点![]() .
.
(1)求证:![]() ,
,![]() 两点中必有一个点坐标是
两点中必有一个点坐标是![]() ;
;
(2)若抛物线的对称轴是![]() ,求其解析式;
,求其解析式;
(3)在(2)的条件下,抛物线上是否存在一点![]() ,使
,使![]() ?如果存在,求出点
?如果存在,求出点![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD内接于⊙O,AC为对角线,∠ACB=∠ACD
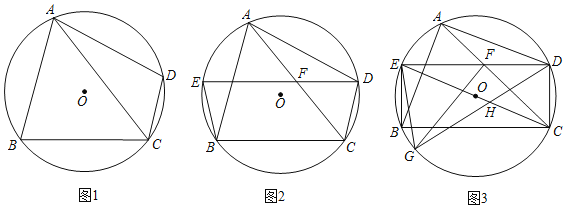
(1)如图1,求证:AB=AD;
(2)如图2,点E在AB弧上,DE交AC于点F,连接BE,BE=DF,求证:DF=DC;
(3)如图3,在(2)的条件下,点G在BC弧上,连接DG,交CE于点H,连接GE,GF,若DE=BC,EG=GH=5,S△DFG=9,求BC边的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】箱子里有4瓶牛奶,其中有一瓶是过期的.现从这4瓶牛奶中任意抽取牛奶饮用,抽取任意一瓶都是等可能的.
(1)若小芳任意抽取1瓶,抽到过期的一瓶的概率是 ;
(2)若小芳任意抽取2瓶,请用画树状图或列表法求,抽出的2瓶牛奶中恰好抽到过期牛奶的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com