
【题目】如图,∠1+∠2=180°,∠DAE=∠BCF,DA平分∠BDF.
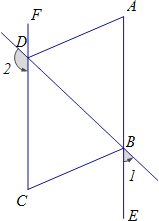
(1)AE与FC会平行吗?说明理由.
(2)AD与BC的位置关系如何?为什么?
(3)BC平分∠DBE吗?为什么?
【答案】(1)平行,理由见解析;(2)平行,理由见解析;(3)平分,理由见解析
【解析】
试题分析:(1)∠1+∠2=180°而∠2+∠CDB=180°,则∠CDB=∠1,根据同位角相等,两直线平行,求得结论;
(2)要说明AD与BC平行,只要说明∠BCF+∠CDA=180°即可.而根据AE∥FC可得:∠CDA+∠DEA=180°,再据∠DAE=∠BCF就可以证得.
(3)BC平分∠DBE即说明∠EBC=∠DBC是否成立.根据AE∥FC,可得:∠EBC=∠BCF,据AD∥BC得到:∠BCF=∠FAD,∠DBC=∠BAD,进而就可以证出结论.
解:(1)平行;
证明:∵∠2+∠CDB=180°,∠1+∠2=180°,
∴∠CDB=∠1,
∴AE∥FC.
(2)平行,
证明:∵AE∥FC,
∴∠CDA+∠DAE=180°,
∵∠DAE=∠BCF
∴∠CDA+∠BCF=180°,
∴AD∥BC.
(3)平分,
证明:∵AE∥FC,
∴∠EBC=∠BCF,
∵AD∥BC,
∴∠BCF=∠FDA,∠DBC=∠BDA,
又∵DA平分∠BDF,即∠FDA=∠BDA,
∴∠EBC=∠DBC,
∴BC平分∠DBE.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:
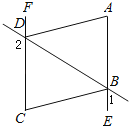
【题目】(14分)探究与发现:如图①,在Rt△ABC中,∠BAC=90°,AB=AC,点D在底边BC上,AE=AD,连结DE.
(1)当∠BAD=60°时,求∠CDE的度数;
(2)当点D在BC (点B、C除外) 上运动时,试猜想并探究∠BAD与∠CDE的数量关系;
(3)深入探究:若∠BAC≠90°,试就图②探究∠BAD与∠CDE的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在ΔABC和ΔDEF中,已知∠C=∠D,∠B=∠E,要判断这两个三角形全等,还需添加条件( )
A. AB=ED B. AB=FD C. AC=FD D. ∠A =∠F.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面推理过程:
如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:
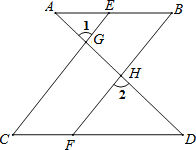
∵∠1=∠2(已知),
且∠1=∠CGD( ),
∴∠2=∠CGD(等量代换).
∴CE∥BF( ).
∴∠ =∠C( ).
又∵∠B=∠C(已知),
∴∠ =∠B(等量代换).
∴AB∥CD( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将∠AOB绕点O顺时针旋转15°,得到∠COD,若∠COD=45°,则∠AOB的度数是( ).
A.15° B.30° C.45° D.60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,我国多个城市遭遇雾霾天气,空气中可吸入颗粒(又称PM2.5)浓度升高,为应对空气污染,小强家购买了空气净化器,该装置可随时显示室内PM2.5的浓度,并在PM2.5浓度超过正常值25(mg/m3)时吸收PM2.5以净化空气.随着空气变化的图象(如图),请根据图象,解答下列问题:
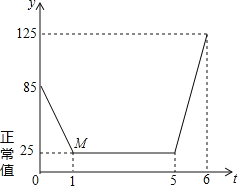
(1)写出题中的变量;
(2)写出点M的实际意义;
(3)求第1小时内,y与t的一次函数表达式;
(4)已知第5﹣6小时是小强妈妈做晚餐的时间,厨房内油烟导致PM2.5浓度升高.若该净化器吸收PM2.5的速度始终不变,则第6小时之后,预计经过多长时间室内PM2.5浓度可恢复正常?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com