
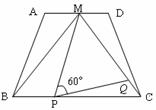
如图,在梯形ABCD中,AD∥BC,AD=2,BC=4,点M是AD的中点,△MBC是等边三角形.动点P、Q分别在线段BC和MC上运动(不与端点重合),且∠MPQ= 60°保持不变.以下四个结论:①梯形ABCD是等腰梯形;②△BMP∽△CPQ;③△MPQ是等边三角形;④)设PC=
60°保持不变.以下四个结论:①梯形ABCD是等腰梯形;②△BMP∽△CPQ;③△MPQ是等边三角形;④)设PC=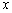 ,MQ=
,MQ=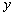 ,则
,则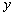 关于
关于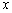 的函数解析式是二次函数.
的函数解析式是二次函数.
(1)判断其中正确的结论是哪几个?
(2)从你认为是正确的结论中选一个加以证明.
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:初中数学 来源: 题型:
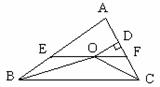
如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D.下列四个结论:①∠BOC=90º+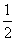 ∠A;②EF不可能是△ABC的中位线;③设OD=m,AE+AF=n,则S△AEF=mn;④以E为圆心、BE为半径的圆与以F为圆心、CF为半径的圆外切. 其中正确结论的个数是( )
∠A;②EF不可能是△ABC的中位线;③设OD=m,AE+AF=n,则S△AEF=mn;④以E为圆心、BE为半径的圆与以F为圆心、CF为半径的圆外切. 其中正确结论的个数是( )
A.1 个 B.2个 C.3个 D.4个
个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
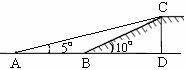 如图,有一段斜坡BC长为10米,坡角∠CBD=10°,为使残疾人的轮椅车通行更省力,现准备把坡角降为5°.
如图,有一段斜坡BC长为10米,坡角∠CBD=10°,为使残疾人的轮椅车通行更省力,现准备把坡角降为5°.
(1)求斜坡新起点A到原起点B的距离;
(2)求坡高CD(结果保留3个有效数字).
参考数据: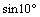 =0.1736 ,
=0.1736 , 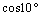 =0.9848,
=0.9848, 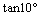 =0.1763
=0.1763
查看答案和解析>>
科目:初中数学 来源: 题型:
在学校组织的实践活动中,小新同学用纸板制作了一个圆锥模型,它的底面半径为1,高为2 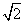 ,则这个圆锥的侧面积是( )
,则这个圆锥的侧面积是( )
A.4π B.3π C.2 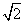 π D.2π
π D.2π
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com