
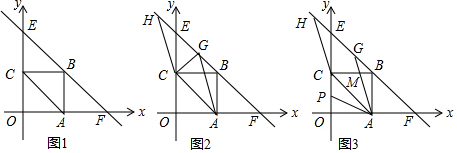
分析 (1)先确定出点A,B,C的坐标,进而求出直线AC的解析式,即可得出结论;
(2)先根据菱形的性质和两点间的距离公式求出点H的坐标,分两种情况构造直角三角形计算;
(3)先求出点G的坐标,进而求出直线AG的解析式,即可求出M的坐标,利用对称确定出点Q的位置,进而求出点Q的坐标即可得出结论.
解答 解:(1)∵正方形ABCD的边长为2,
∴A(2,0),C(0,2),B(2,2),
∴直线AC的解析式为y=-x+2,
∵EF∥AC,
∴设直线EF的解析式为y=-x+b,
∵点B在直线EF上,
∴2=-2+b,
∴b=4,
∴直线EF的解析式为y=-x+4;
(2)∵A(2,0),C(0,2),
∴AC=2$\sqrt{2}$,
∵四边形ACHG是菱形,
∴CH=AC=2$\sqrt{2}$,
∵点H在直线EF上,
∴设H(m,-m+4),
∵C(0,2),
∴CH=$\sqrt{{m}^{2}+(m-2)^{2}}$,
∴$\sqrt{{m}^{2}+(m-2)^{2}}$=2$\sqrt{2}$,
∴m=1±$\sqrt{3}$,
∴H(1-$\sqrt{3}$,3+$\sqrt{3}$)或(1+$\sqrt{3}$,3-$\sqrt{3}$),
①当点H(1-$\sqrt{3}$,3+$\sqrt{3}$)时,
如图2,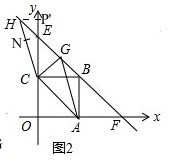 过点H作HP'⊥y轴于P',
过点H作HP'⊥y轴于P',
∴HP'=$\sqrt{3}$-1,
∵C(0,2),
∴CP'=$\sqrt{3}$+1,
在Rt△CHP'中,tan∠HCP'=$\frac{HP'}{CP'}$=$\frac{\sqrt{3}-1}{\sqrt{3}+1}$=2-$\sqrt{3}$,
过点E作EN⊥CH,
∴tan∠HCM=$\frac{EN}{CH}$=2-$\sqrt{3}$,
∴EN=(2-$\sqrt{3}$)CN,
∴CN=(2+$\sqrt{3}$)EN,
∵CE=2,
根据勾股定理得,CN2+EN2=CE2,
∴[(2+$\sqrt{3}$)EN]2+EN2=4,
∴EN2=2-$\sqrt{3}$,
在Rt△EHP中,∠HEP'=45°,EP'=3+$\sqrt{3}$-4=$\sqrt{3}$-1,
∴EH2=2($\sqrt{3}$-1)2=4(2-$\sqrt{3}$)
在Rt△EHN中,sin∠EHN=$\frac{EN}{HE}$=$\sqrt{(\frac{EN}{HE}})^{2}$=$\sqrt{\frac{E{N}^{2}}{H{E}^{2}}}$=$\sqrt{\frac{2-\sqrt{3}}{4(2-\sqrt{3})}}$=$\frac{1}{2}$,
∴∠EHN=30°,
∴∠ACH=180°-30=150°,
②当H(1+$\sqrt{3}$,3-$\sqrt{3}$)时,如图1,同①的方法可得,∠ACH=30°.
即:当∠ACH的度数为30°或150°时,四边形ACHG是菱形;
(3)∵点G在x轴上方,
∴菱形的内角∠ACH=150°,即:图2的图形情况,
如图3,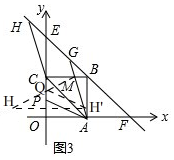
由(2)知,H(1-$\sqrt{3}$,3+$\sqrt{3}$),
∴G(3-$\sqrt{3}$,1+$\sqrt{3}$),
∴直线AG的解析式为y=-(2+$\sqrt{3}$)x+2(2+$\sqrt{3}$),
∴M(7-4$\sqrt{3}$,2),
在线段AB上取一点H'使AH'=2-$\sqrt{3}$,
∴H'(2,2-$\sqrt{3}$),
∴点H关于y轴的对称点H(-2,2-$\sqrt{3}$),
连接MH,MH于y轴的交点就是Q,此时四边形AMQP的周长最小
∵H(-2,2-$\sqrt{3}$),M(7-4$\sqrt{3}$,2),
∴直线HM的解析式为y=$\frac{3\sqrt{3}-4}{11}$x+$\frac{14-5\sqrt{3}}{11}$,
∴Q(0,$\frac{14-5\sqrt{3}}{11}$),
∴P(0,$\frac{6\sqrt{3}-8}{11}$).
点评 此题是一次函数综合题,主要考查了待定系数法,正方形的性质,两点间的距离公式,锐角三角函数,对称的性质,勾股定理,解(1)的关键是求出直线AC的解析式,解(2)的关键是得出点H的坐标,解(3)的关键是构造出图形找出点Q的位置,是一道涉及知识点比较多,计算量比较大的中考常考题.


科目:初中数学 来源: 题型:解答题
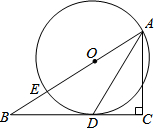 如图,在△ABC中,∠C=90°,点E在AB上,以AE为直径的⊙O与BC相切于点D,连接AD.
如图,在△ABC中,∠C=90°,点E在AB上,以AE为直径的⊙O与BC相切于点D,连接AD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
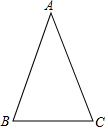 如图,在△ABC中,AB=AC.
如图,在△ABC中,AB=AC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在?ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,AE与BF相交于点O,连接EF.
如图,在?ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,AE与BF相交于点O,连接EF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com