
| 植树品种 | 甲种 | 乙种 | 丙种 | 丁种 |
| 植树棵数 | 150 | 125 | 125 |
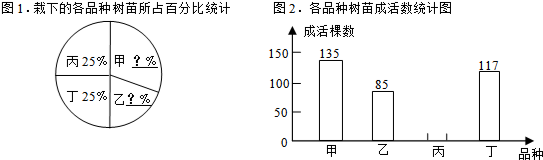
分析 (1)根据丙种植树125棵,占总数的25%,即可求得总棵树,然后求得乙种的棵树;
(2)利用百分比的意义即可求得甲和乙所占的百分比;
(3)求得成活的总棵树,然后求得丙成活的棵树求解.
解答 解:(1)这次栽下的四个品种的树苗总棵树是:125÷25%=500(棵),
则乙品种树苗的棵树是:500-150-125-125=100(棵);
(2)甲所占的百分比是:$\frac{150}{500}$×100%=30%,
乙所占的百分比是:$\frac{100}{500}$×100%=20%;
(3)成活的总棵树是:500×90%=450(棵),
450-135-85-117=113(棵),
如图所示:
故答案为:500,100;30,20.
点评 本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.


科目:初中数学 来源: 题型:解答题
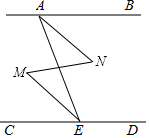 如图,∠BAE+∠AED=180°,∠M=∠N.求证:∠BAN=∠CEM.
如图,∠BAE+∠AED=180°,∠M=∠N.求证:∠BAN=∠CEM.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
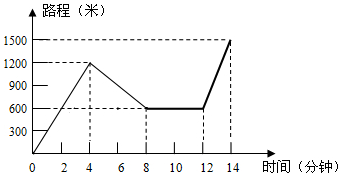 小红星期天从家里出发骑车去舅舅家做客,当她骑了一段路时,想起要买个礼物送给表弟,于是又折回到刚经过的一家商店,买好礼物后又继续骑车去舅舅家,以下是她本次去舅舅家所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题:
小红星期天从家里出发骑车去舅舅家做客,当她骑了一段路时,想起要买个礼物送给表弟,于是又折回到刚经过的一家商店,买好礼物后又继续骑车去舅舅家,以下是她本次去舅舅家所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
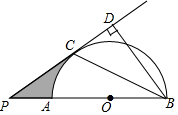 如图,AB是半圆O的直径,点P在BA的延长线上,PD切⊙O于点C,BD⊥PD,垂足为D,连接BC
如图,AB是半圆O的直径,点P在BA的延长线上,PD切⊙O于点C,BD⊥PD,垂足为D,连接BC查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (a+2)2=a2+4 | B. | x3+x2=x5 | C. | $\frac{2}{2x+y}$=$\frac{1}{x+y}$ | D. | (-3a3)2=9a6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
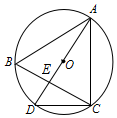 如图,⊙O是△ABC的外接圆,直径AD与BC相交于点E,连接CD,若⊙O的半径为5,AB=AC=8,DE=3,则EC长为( )
如图,⊙O是△ABC的外接圆,直径AD与BC相交于点E,连接CD,若⊙O的半径为5,AB=AC=8,DE=3,则EC长为( )| A. | 4 | B. | $\frac{21}{4}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com