
【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AEF,延长EF交边BC于点G,连结AG,CF,则下列结论:①△ABG≌△AFG;②BG=CG;③AG∥CF;④S△EGC=S△AFE;⑤S△FGC=![]() ;其中正确的结论有_____.
;其中正确的结论有_____.

【答案】①②③④⑤
【解析】
由正方形和折叠的性质得出AF=AB,∠B=∠AFG=90°,由HL即可证明Rt△ABG≌Rt△AFG,得出①正确,设BG=x,则CG=BC-BG=6-x,GE=GF+EF=BG+DE=x+2,由勾股定理求出x=3,得出②正确;由等腰三角形的性质和外角关系得出∠AGB=∠FCG,证出平行线,得出③正确;分别求出△EGC,△AEF的面积,可以判断④,由![]()
,可求出△FGC的面积,故此可对⑤做出判断.
解:解:∵四边形ABCD是正方形,
∴AB=AD=DC=6,∠B=D=90°,
∵CD=3DE,
∴DE=2,
∵△ADE沿AE折叠得到△AFE,
∴DE=EF=2,AD=AF,∠D=∠AFE=∠AFG=90°,
∴AF=AB,
∵在Rt△ABG和Rt△AFG中,
![]() ,
,
∴Rt△ABG≌Rt△AFG(HL).
∴①正确;
∵Rt△ABG≌Rt△AFG,
∴BG=FG,∠AGB=∠AGF.
设BG=x,则CG=BC-BG=6-x,GE=GF+EF=BG+DE=x+2.
在Rt△ECG中,由勾股定理得:CG2+CE2=EG2.
∵CG=6-x,CE=4,EG=x+2,
∴(6-x)2+42=(x+2)2,解得:x=3.
∴BG=GF=CG=3.
∴②正确;
∵CG=GF,
∴∠CFG=∠FCG.
∵∠BGF=∠CFG+∠FCG,∠BGF=∠AGB+∠AGF,
∴∠CFG+∠FCG=∠AGB+∠AGF.
∵∠AGB=∠AGF,∠CFG=∠FCG,
∴∠AGB=∠FCG.
∴AG∥CF.
∴③正确;
∵S△EGC=![]() ×3×4=6,S△AEF=S△ADE=
×3×4=6,S△AEF=S△ADE=![]() ×6×2=6,
×6×2=6,
∴S△EGC=S△AFE;
∴④正确,
∵△CFG和△CEG中,分别把FG和GE看作底边,
则这两个三角形的高相同.
∴![]() ,
,
∵S△GCE=6,
∴S△CFG=![]() ×6=3.6,
×6=3.6,
∴⑤正确;
故答案为①②③④⑤.


科目:初中数学 来源: 题型:
【题目】5月16日,我校进行了全校师生防灾减灾大演练,警报拉响后同学们匀速跑步到操场,在操场指定位置清点人数、听广播后,再沿原路匀速步行回教室,同学们离开教学楼的距离y与时间x的关系的大致图象是( )
A.  B.
B.  C.
C.  D.
D. 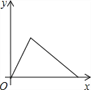
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把长为40cm,宽30cm的长方形硬纸板,剪掉2个小正方形和2个小长方形(阴影部分即剪掉的部分),将剩余的部分拆成一个有盖的长方体盒子,设剪掉的小正方形边长为xcm(纸板的厚度忽略不计)
(1)长方体盒子的长、宽、高分别为多少?(单位:cm)
(2)若折成的一个长方体盒于表面积是950cm2 , 求此时长方体盒子的体积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,E为AC的中点,AD平分∠BAC,BA:CA=2:3,AD与BE相交于点O,若△OAE的面积比△BOD的面积大1,则△ABC的面积是( )

A. 8 B. 9 C. 10 D. 11
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有下列四个条件:①AB=BC,②∠ABC=90![]() ,③AC=BD,④AC⊥BD.从中选取两个作为补充条件,使□BCD为正方形(如图).现有下列四种选法,其中错误的是 ( )
,③AC=BD,④AC⊥BD.从中选取两个作为补充条件,使□BCD为正方形(如图).现有下列四种选法,其中错误的是 ( )
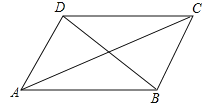
A. ②③ B. ②④ C. ①② D. ①③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场的一种书法笔每只售价25元,书法练习本每本售价5元。为促销,商场制定了两种优惠方案:买一支书法笔就赠送一本书法练习本;方案二:按够买金额的九折付款,我校书法社团够买10支书法笔,x(x>10)本练习本。
(1)请你写出两种优惠方案的实际付款金额y(元)与x(本)之间的关系式。
(2)当购买多少本书法练习本时,两种优惠方案的实付金额一样?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在作二次函数y1=ax2+bx+c与一次函数y2=kx+m的图象时,先列出下表:
x | … | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 | … |
y1 | … | 0 | ﹣3 | ﹣4 | ﹣3 | 0 | 5 | 12 | … |
y2 | … | 0 | 2 | 4 | 6 | 8 | 10 | 12 | … |
请你根据表格信息回答下列问题,
(1)二次函数y1=ax2+bx+c的图象与y轴交点坐标为;
(2)当y1>y2时,自变量x的取值范围是;
(3)请写出二次函数y1=ax2+bx+c的三条不同的性质.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线的顶点D的坐标为(1,﹣4),与y轴交于点C(0,﹣3),与x轴交于A、B两点.
(1)求该抛物线的函数关系式;
(2)在抛物线上存在点P(不与点D重合),使得S△PAB=S△ABD , 请求出P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进甲,乙两种商品,若购买6件甲商品和3件乙商品共用108元;若购买5件甲商品和2件乙商品共用88元.
(1)求甲,乙两种商品每件的价格;
(2)已知该商店购买乙商品的件数比购买甲商品的件数多8件,如果需要购买甲,乙两种商品的总件数不少于32件,且商店购买的甲、乙两种商品的总费用不超过292元,那么该商店有哪几种购买方案?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com