
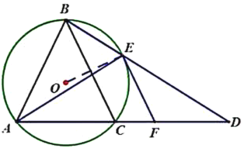
【题目】如图,![]() 是
是![]() 的外接圆,
的外接圆,![]() ,延长
,延长![]() 到点
到点![]() ,使得
,使得![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 做
做![]() 的平行线交
的平行线交![]() 于点
于点![]() .
.

(1)求证:![]() ;
;
(2)求证:![]() 为
为![]() 的切线;
的切线;
(3)若![]() ,
,![]() ,求弦
,求弦![]() 的长.
的长.
【答案】(1)证明见解析;(2)证明见解析;(2)AC=![]() .
.
【解析】
(1)由等腰三角形的性质可得∠DBC=∠BDC,根据圆周角定理可得∠DBC=∠CAE,即可证明∠BDC=∠CAE,进而可证明AE=DE;
(2)如图,连接OE,根据圆周角定理及三角形外角性质可得∠ACB=2∠EAC,根据等腰三角形的性质可得∠BAC=2∠EAC,进而可证明点E为![]() 的中点,根据垂径定理推论可得OE⊥BC,根据EF//BC可得OE⊥EF,即可证明EF是⊙O的切线;
的中点,根据垂径定理推论可得OE⊥BC,根据EF//BC可得OE⊥EF,即可证明EF是⊙O的切线;
(3)由∠ABE=∠DAB,∠BAE=∠BDA可证明![]() ,根据相似三角形的性质可求出BD的长,进而可求出DE的长,由(1)可得AE=DE,根据相似三角形的性质即可求出AD的长,根据AB=BC=CD,利用线段的和差关系即可求出AC的长.
,根据相似三角形的性质可求出BD的长,进而可求出DE的长,由(1)可得AE=DE,根据相似三角形的性质即可求出AD的长,根据AB=BC=CD,利用线段的和差关系即可求出AC的长.
(1)∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
(2)如图,连接![]() ,
,
∵∠DBC=∠BDC,
∴∠ACB=2∠DBC,
∵∠DBC=∠EAC,
∴∠ACB=2∠EAC,
∵AB=BC,
∴∠BAC=∠ACB,
∴∠BAC=2∠EAC,
∴∠EAC=∠EAB,
∴点![]() 为
为![]() 的中点,
的中点,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() 为圆
为圆![]() 的切线.
的切线.
(3)在![]() 和
和![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵AB=5,BE=3,
∴![]()
∴![]() ,
,
由(1)得![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】某微商销售的某商品每袋成本20元,设销售价格为x(单位:元/袋),该微商发现销售量y与销售价格x之间的关系如表:
销售价格x(元/袋) | 25 | 30 | 35 | 40 |
销售件数y | 275 | 250 | 225 | 200 |
(1)求y关于x的函数表达式;
(2)根据物价部门的规定,商品的利润率不能超过100%,该微商应该如何定价,才能使获得的利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连接AO,如果AB=4,AO=6![]() ,那么AC=_____.
,那么AC=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市今年中考理化实验操作考试,采用学生抽签方式决定自己的考试内容.规定:每位考生必须在三个物理实验(用纸签A、B、C表示)和三个化学实验(用纸签D、E、F表示)中各抽取一个进行考试,小刚在看不到纸签的情况下,分别从中各随机抽取一个.
(1) 用“列表法”或“树状图法”表示所有可能出现的结果;
(2) 小刚抽到物理实验B和化学实验F(记作事件P)的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() 为直径,
为直径,![]() 弦,
弦,![]() 垂足为
垂足为![]() ,且
,且![]() 为
为![]() 的中点,连接
的中点,连接![]() .
.
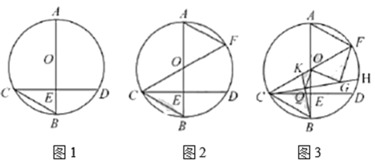
(1)如图1,求![]() 的度数.
的度数.
(2)如图2,连接![]() 并延长,交圆
并延长,交圆![]() 于点
于点![]() ,连接
,连接![]() ,求证:
,求证:![]()
(3)在(2)问的条件下,![]() 为弧
为弧![]() 上的一点,连接
上的一点,连接![]() ,
,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 上的一点,连接
上的一点,连接![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() ,若
,若![]() ,
,![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同学们参加综合实践活动时,看到木工师傅用“三弧法”在板材边角处作直角,其作法是:如图:
(1)作线段AB,分别以点A,B为圆心,AB长为半径作弧,两弧交于点C;
(2)以点C为圆心,仍以AB长为半径作弧交AC的延长线于点D;
(3)连接BD,BC.
根据以上作图过程及所作图形,下列结论中错误的是( )

A.∠ABD=90°B.CA=CB=CDC.sinA=![]() D.cosD=
D.cosD=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,大楼AD与塔CB之间的距离AC长为27m,某人在楼底A处测得塔顶的仰角为60°,爬到楼顶D处测得塔顶B的仰角为30°,分别求大楼AD的高与塔BC的高(结果精确到0.1m,参考数据:![]() ≈2.24,
≈2.24,![]() ≈1.732,
≈1.732,![]() ≈1.414)
≈1.414)

查看答案和解析>>
科目:初中数学 来源: 题型:
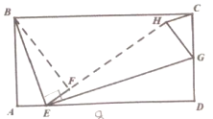
【题目】如图,矩形ABCD中,AB=4,AD=8,点E为AD上一点,将△ABE沿BE折叠得到△FBE,点G为CD上一点,将△DEG沿EG折叠得到△HEG,且E、F、H三点共线,当△CGH为直角三角形时,AE的长为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com