

分析 (1)根据“同角的补角相等”求证.
(2)可先进行分析:因为∠ACB+∠ECD=∠ACE+∠ECD+∠DCB+∠ECD=∠ACD+∠ECB,故∠ACB与∠ECD数量关系:∠ACB+∠ECD=180°.
(3)作图后根据两直线平行的判定定理去求证.
解答 (1)证明;∵∠ACD=∠ECB=90°,
∴∠ACE=∠ACD-∠ECD=90°-∠ECD,
∠BCD=∠ECB-∠ECD=90°-∠ECD,
∴∠ACE=∠BCE.
(2)猜想:∠ACB+∠ECD=180°.
理由:∵∠ACD=∠ECB=90°,
∴∠ACB+∠ECD
=∠ACE+∠ECD+∠DCB+∠ECD
=∠ACD+∠ECB
=90°+90°=180°
(3)当∠ACB=120°或60°时,AD∥CB.
理由:如图①,根据“同旁内角互补,两直线平行”:
当∠A+∠ACB=180°时,AD∥BC,
此时,∠ACB=180°-∠A=180°-60°=120°.
如图②,根据“内错角相等,两直线平行”:
当∠ACB=∠A=60°时,AD∥BC.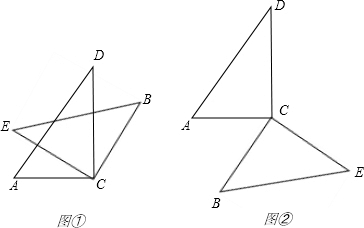
点评 本题考查了图形的旋转及平行线的判定,解题的关键是将实物在变换时相应的几何图形作出来.


科目:初中数学 来源: 题型:选择题
| A. | 3cm | B. | 6cm | C. | 13cm | D. | 5.5cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 已知如图,AB是半圆O的直径,弦AD、BC相交于点P,那么$\frac{CD}{AB}$等于∠BPD的( )
已知如图,AB是半圆O的直径,弦AD、BC相交于点P,那么$\frac{CD}{AB}$等于∠BPD的( )| A. | 正弦 | B. | 余弦 | C. | 正切 | D. | 以上都不对 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
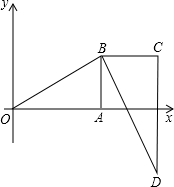 如图,已知△OAB,将△OAB绕点B逆时针方向旋转90°到△DCB且A、B点的坐标分别为A(2,0),B(2,1),其中O的对应点为点D,求过点O、B、D的抛物线的解析式.
如图,已知△OAB,将△OAB绕点B逆时针方向旋转90°到△DCB且A、B点的坐标分别为A(2,0),B(2,1),其中O的对应点为点D,求过点O、B、D的抛物线的解析式.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如果小球在如图所示的七巧板上自由滚动,并随机停留在这七巧板的某个位置上(不考虑停在边线的情况),那么它最终停留在四边形EFLH的概率是$\frac{1}{8}$.
如果小球在如图所示的七巧板上自由滚动,并随机停留在这七巧板的某个位置上(不考虑停在边线的情况),那么它最终停留在四边形EFLH的概率是$\frac{1}{8}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
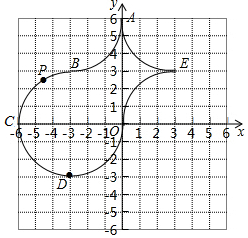 如图,在平面直角坐标系xOy中,几段$\frac{1}{4}$圆弧(占圆周的$\frac{1}{4}$的圆弧)首尾连接围成的封闭区域形如“宝瓶”,其中圆弧连接点都在正方形网格的格点处,点A的坐标是A(0,6),点C的坐标是C(-6,0).
如图,在平面直角坐标系xOy中,几段$\frac{1}{4}$圆弧(占圆周的$\frac{1}{4}$的圆弧)首尾连接围成的封闭区域形如“宝瓶”,其中圆弧连接点都在正方形网格的格点处,点A的坐标是A(0,6),点C的坐标是C(-6,0).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 △ABC中,∠B=90°,AB=6cm,BC=8cm.将△ABC沿射线BC方向平移10cm,得到△DEF,A,B,C的对应点分别是D,E,F,则下列说法错误的是( )
△ABC中,∠B=90°,AB=6cm,BC=8cm.将△ABC沿射线BC方向平移10cm,得到△DEF,A,B,C的对应点分别是D,E,F,则下列说法错误的是( )| A. | 四边形ABED是矩形 | B. | AD${\;}_{=}^{∥}$CF | ||
| C. | BC=CF | D. | DF=CF |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com