
| A�� | ʵ��ÿ��ȼƻ�����ɸ�������300m��ʵ�����������Ǽƻ���$\frac{2}{3}$ | |
| B�� | ʵ��ÿ��ȼƻ�����ɸ�������300m���ƻ�����������ʵ�ʵ�$\frac{2}{3}$ | |
| C�� | ʵ��ÿ��ȼƻ�����ɸ�������300m���ƻ�����������ʵ�ʵ�$\frac{2}{3}$ | |
| D�� | ʵ��ÿ��ȼƻ�����ɸ�������300m��ʵ�����������Ǽƻ���$\frac{2}{3}$ |
���� �������з��̵õ�������ϵ����ϵ�����ϵ������ȷ��ѡ��
��� �⣺�ƻ�ÿ������̻�����������xm����x+300����ʾʵ��ÿ��ȼƻ�����ɸ�������300m��
$\frac{12000}{x}$��$\frac{12000}{x+300}$���DZ�ʾ�Ĺ���ʱ�䣬
���Ե�x����ķ���Ϊ$\frac{2}{3}$��$\frac{12000}{x}$=$\frac{12000}{x+300}$ʱ��ʵ��ÿ��ȼƻ�����ɸ�������300m��ʵ�����������Ǽƻ���$\frac{2}{3}$��
��ѡ��A��
���� ���⿼���˷�ʽ���̵�Ӧ�ã��з��̽�Ӧ����Ĺؼ�������������ȹ�ϵ���ҵ��ؼ�������ҵ�������ϵ�ǽ������Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
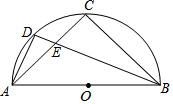 ��ͼ��AB�ǰ�ԲO��ֱ����C��$\widehat{AB}$���е㣬D��$\widehat{AC}$���е㣬AC��BD�ཻ�ڵ�E��
��ͼ��AB�ǰ�ԲO��ֱ����C��$\widehat{AB}$���е㣬D��$\widehat{AC}$���е㣬AC��BD�ཻ�ڵ�E���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a��$\frac{3}{2}$ | B�� | a��$\frac{3}{2}$ | C�� | a��$\frac{3}{2}$��a��1 | D�� | a$��\frac{3}{2}$��a��1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com