

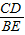 =
=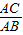 ,∠ACD=∠ABE,由k≠1,则BE≠CD.从而得出①不成立;可证明CD⊥BE,则②成立.
,∠ACD=∠ABE,由k≠1,则BE≠CD.从而得出①不成立;可证明CD⊥BE,则②成立.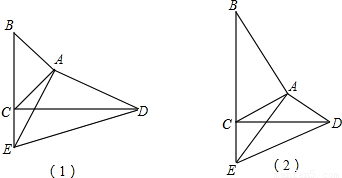 解:(1)如图(1),∵∠DAE=∠BAC=90°,
解:(1)如图(1),∵∠DAE=∠BAC=90°,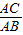 =
=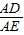 =
=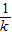 .
.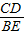 =
=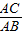 ,∠ACD=∠ABE.
,∠ACD=∠ABE.

科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 予证明;若不成立,请说明理由.
予证明;若不成立,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
如图1,小明将一张长方形纸片沿对角线剪开,得到两张三角形纸片(如图2)量得它们的斜边长为10cm,较小锐角为30°再将这两张三角形纸片摆成如图3的形状,但点B、C、F、D在同一条直线上,且点C与点F重合(在图3至图6中统一用F表示).
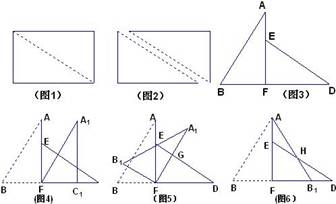
小明在对这两张三角形纸片进行如下操作时遇到了三个问题,请你帮忙解决.
1.(1)将图3中的△ABC沿BD向右平移到图4的位置,使点B与点F重合,请你求出平移的距离;
2.(2)将图3中的△ABC绕点F顺时针方向旋转30°到图5的位置,A1F交DE于G,若DG=kEG,求k的值;
3.(3)将图3中的△ABF沿直线AF翻折到图6的位置,AB1交DE于点H,请证明:AH=DH.
查看答案和解析>>
科目:初中数学 来源:2011年重庆市石柱县九年级期末考试数学卷 题型:解答题
如图1,小明将一张长方形纸片沿对角线剪开,得到两张三角形纸片(如图2)量得它们的斜边长为10cm,较小锐角为30°再将这两张三角形纸片摆成如图3的形状,但点B、C、F、D在同一条直线上,且点C与点F重合(在图3至图6中统一用F表示).

小明在对这两张三角形纸片进行如下操作时遇到了三个问题,请你帮忙解决.
1.(1)将图3中的△ABC沿BD向右平移到图4的位置,使点B与点F重合,请你求出平移的距离;
2.(2)将图3中的△ABC绕点F顺时针方向旋转30°到图5的位置,A1F交DE于G,若DG=kEG,求k的值;
3.(3)将图3中的△ABF沿直线AF翻折到图6的位置,AB1交DE于点H,请证明:AH=DH.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com