
 如图,已知?OABC,在平面直角坐标系中,A(5,0),C(1,3),直线y=kx-2与BC、OA分别交于M,N,且将?OABC的面积分成相等的两部分,则k的值是k=$\frac{7}{6}$.
如图,已知?OABC,在平面直角坐标系中,A(5,0),C(1,3),直线y=kx-2与BC、OA分别交于M,N,且将?OABC的面积分成相等的两部分,则k的值是k=$\frac{7}{6}$. 分析 根据平行四边形的性质得AC的中点为平行四边形的对角线的交点,则利用线段的中点坐标公式得到平行四边形ABCO的对角线的交点坐标为(3,$\frac{3}{2}$),然后把(3,$\frac{3}{2}$)y=kx-2可得到k的值.
解答 解:∵四边形ABCO为平行四边形,
∴AC的中点为平行四边形的对角线的交点,
而A(5,0),C(1,3),
∴平行四边形ABCO的对角线的交点坐标为(3,$\frac{3}{2}$),
∵直线y=kx-2将?OABC的面积分成相等的两部分,
∴直线y=kx-2经过点(3,$\frac{3}{2}$),
∴3k-2=$\frac{3}{2}$,解得k=$\frac{7}{6}$.
故答案为k=$\frac{7}{6}$.
点评 本题考查了待定系数法求一次函数解析式:先设出函数的一般形式,如求一次函数的解析式时,先设y=kx+b;将自变量x的值及与它对应的函数值y的值代入所设的解析式,得到关于待定系数的方程或方程组;解方程或方程组,求出待定系数的值,进而写出函数解析式.也考查了平行四边形的性质.


科目:初中数学 来源: 题型:解答题
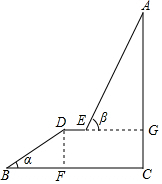 如图,A为某旅游景区的最佳观景点,游客可从B处乘坐缆车先到达小观景平台DE观景,然后再由E处继续乘坐缆车达到A处,返程时从A处乘坐升降电梯直接到达C处;已知:AC⊥BC于C,DE∥BC,BC=110米,DE=10米,BD=60米,BD=60米,α=30°,β=60°,求AC的高度.
如图,A为某旅游景区的最佳观景点,游客可从B处乘坐缆车先到达小观景平台DE观景,然后再由E处继续乘坐缆车达到A处,返程时从A处乘坐升降电梯直接到达C处;已知:AC⊥BC于C,DE∥BC,BC=110米,DE=10米,BD=60米,BD=60米,α=30°,β=60°,求AC的高度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
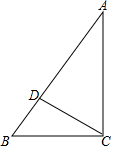 如图,在Rt△ABC中,∠ACB=90°,点D在AB上,将△BCD绕点C按顺时针方向旋转90°后得△ECF.
如图,在Rt△ABC中,∠ACB=90°,点D在AB上,将△BCD绕点C按顺时针方向旋转90°后得△ECF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
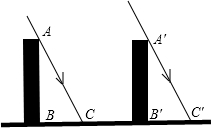 如图,太阳光线AC与A′C′是平行的,同一时刻垂直于地面的两根木杆在太阳光照射下的影子一样长,那么这辆跟木杆高度相同吗?
如图,太阳光线AC与A′C′是平行的,同一时刻垂直于地面的两根木杆在太阳光照射下的影子一样长,那么这辆跟木杆高度相同吗?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,OA⊥OB,OA=45cm,OB=15cm,一机器人在B处发现有一个小球自A点出发沿着AO方向匀速滚向点O,机器人立即从B处出发以相同的速度匀速直线前进去拦截小球,在点C处截住了小球,求机器人行走的路程BC.
如图所示,OA⊥OB,OA=45cm,OB=15cm,一机器人在B处发现有一个小球自A点出发沿着AO方向匀速滚向点O,机器人立即从B处出发以相同的速度匀速直线前进去拦截小球,在点C处截住了小球,求机器人行走的路程BC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
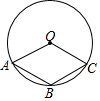 如图,已知点A,B,C均在⊙O上,并且四边形OABC是菱形,那么∠AOC与2∠OAB之间的关系是( )
如图,已知点A,B,C均在⊙O上,并且四边形OABC是菱形,那么∠AOC与2∠OAB之间的关系是( )| A. | ∠AOC>2∠OAB | B. | ∠AOC=2∠OAB | C. | ∠AOC<2∠OAB | D. | 不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com