
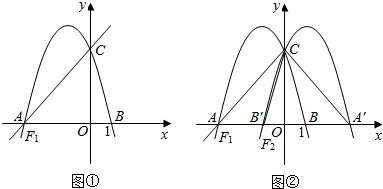
分析 (1)利用一次函数的解析式求出点A、C的坐标,然后再利用B点坐标即可求出二次函数的解析式;
(2)由于M在抛物线F1上,所以可设M(a,-$\frac{4}{3}$a2-$\frac{8}{3}$a+4),然后分别计算S四边形MAOC和S△BOC,过点M作MP⊥x轴于点P,则S四边形MAOC的值等于△APM的面积与梯形POCM的面积之和.
(3)由于没有说明点P的具体位置,所以需要将点P的位置进行分类讨论,当点P在A′的右边时,此情况是不存在;当点P在A′的左边时,此时∠DA′P=∠CAB′,若以A′、D、P为顶点的三角形与△AB′C相似,则分为以下两种情况进行讨论:①$\frac{DA′}{PA′}$=$\frac{AC}{AB′}$;②$\frac{DA′}{PA′}$=$\frac{AB′}{AC}$.
解答 解:(1)令y=0代入y=$\frac{4}{3}$x+4,
∴x=-3,
A(-3,0),
令x=0,代入y=$\frac{4}{3}$x+4,
∴y=4,
∴C(0,4),
设抛物线F1的解析式为:y=a(x+3)(x-1),
把C(0,4)代入上式得,a=-$\frac{4}{3}$,
∴y=-$\frac{4}{3}$x2-$\frac{8}{3}$x+4,
(2)如图①,设点M(a,-$\frac{4}{3}$a2-$\frac{8}{3}$a+4)
其中-3<a<0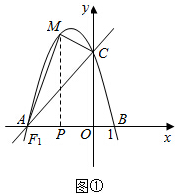
∵B(1,0),C(0,4),
∴OB=1,OC=4
∴S△BOC=$\frac{1}{2}$OB•OC=2,
过点M作MP⊥x轴于点P,
∴MP=-$\frac{4}{3}$a2-$\frac{8}{3}$a+4,AP=a+3,OP=-a,
∴S四边形MAOC=$\frac{1}{2}$AP•MP+$\frac{1}{2}$(MP+OC)•OP
=$\frac{1}{2}$AP•MP+$\frac{1}{2}$OP•MP+$\frac{1}{2}$OP•OC
=$\frac{1}{2}MP(AP+OP)$+$\frac{1}{2}OP•OC$
=$\frac{1}{2}MP•OA$+$\frac{1}{2}OP•OC$
=$\frac{1}{2}$×3(-$\frac{4}{3}$a2-$\frac{8}{3}$a+4)+$\frac{1}{2}$×4×(-a)
=-2a2-6a+6
∴S=S四边形MAOC-S△BOC
=(-2a2-6a+6)-2
=-2a2-6a+4
=-2(a+$\frac{3}{2}$)2+$\frac{17}{2}$
∴当a=-$\frac{3}{2}$时,
S有最大值,最大值为$\frac{17}{2}$
此时,M(-$\frac{3}{2}$,5);
(3)如图②,由题意知:M′($\frac{3}{2},5$),B′(-1,0),A′(3,0)
∴AB′=2,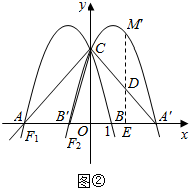
设直线A′C的解析式为:y=kx+b,
把A′(3,0)和C(0,4)代入y=kx+b,
得:$\left\{\begin{array}{l}{b=4}\\{0=3k+b}\end{array}\right.$,
∴$\left\{\begin{array}{l}{k=-\frac{4}{3}}\\{b=4}\end{array}\right.$
∴y=-$\frac{4}{3}$x+4,
令x=$\frac{3}{2}$代入y=-$\frac{4}{3}$x+4,
∴y=2
∴$D(\frac{3}{2},2)$
由勾股定理分别可求得:AC=5,DA′=$\frac{5}{2}$
设P(m,0)
当m<3时,
此时点P在A′的左边,
∴∠DA′P=∠CAB′,
当$\frac{DA′}{PA′}$=$\frac{AC}{AB′}$时,△DA′P∽△CAB′,
此时,$\frac{5}{2}$=$\frac{5}{2}$(3-m),
解得:m=2,
∴P(2,0)
当$\frac{DA′}{PA′}$=$\frac{AB′}{AC}$时,△DA′P∽△B′AC,
此时,$\frac{5}{2}$=$\frac{2}{5}$(3-m)
m=-$\frac{13}{4}$,
∴P(-$\frac{13}{4}$,0)
当m>3时,
此时,点P在A′右边,
由于∠CB′O≠∠DA′E,
∴∠AB′C≠∠DA′P
∴此情况,△DA′P与△B′AC不能相似,
综上所述,当以A′、D、P为顶点的三角形与△AB′C相似时,点P的坐标为(2,0)或(-$\frac{13}{4}$,0).
点评 本题是二次函数的综合问题,涉及待定系数法求解析式,二次函数最值问题,相似三角形的判定与性质等知识内容,综合程度较大,需要学生灵活运用所学知识解决问题.另外对于动点问题,通常可以用一参数m来表示该动点.


科目:初中数学 来源: 题型:选择题
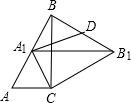 如图,Rt△ABC中,∠C=90°,∠ABC=30°,AC=2,△ABC绕点C顺时针旋转得△A1B1C,当A1落在AB边上时,连接B1B,取BB1的中点D,连接A1D,则A1D的长度是( )
如图,Rt△ABC中,∠C=90°,∠ABC=30°,AC=2,△ABC绕点C顺时针旋转得△A1B1C,当A1落在AB边上时,连接B1B,取BB1的中点D,连接A1D,则A1D的长度是( )| A. | $\sqrt{7}$ | B. | 2$\sqrt{2}$ | C. | 3 | D. | 2$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
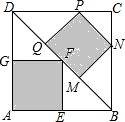 如图,在正方形ABCD中,点E,N,P,G分别在边AB,BC,CD,DA上,点M,F,Q都在对角线BD上,且四边形MNPQ和AEFG均为正方形,则$\frac{{S}_{正方形MNPQ}}{{S}_{正方形AEFG}}$的值等于$\frac{8}{9}$.
如图,在正方形ABCD中,点E,N,P,G分别在边AB,BC,CD,DA上,点M,F,Q都在对角线BD上,且四边形MNPQ和AEFG均为正方形,则$\frac{{S}_{正方形MNPQ}}{{S}_{正方形AEFG}}$的值等于$\frac{8}{9}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
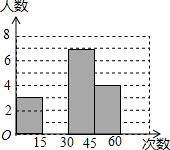 在大课间活动中,体育老师随机抽取了七年级甲、乙两班部分女学生进行仰卧起坐的测试,并对成绩进行统计分析,绘制了频数分布表和统计图,请你根据图表中的信息完成下列问题:
在大课间活动中,体育老师随机抽取了七年级甲、乙两班部分女学生进行仰卧起坐的测试,并对成绩进行统计分析,绘制了频数分布表和统计图,请你根据图表中的信息完成下列问题:| 分 组 | 频数 | 频率 |
| 第一组(0≤x<15) | 3 | 0.15 |
| 第二组(15≤x<30) | 6 | a |
| 第三组(30≤x<45) | 7 | 0.35 |
| 第四组(45≤x<60) | b | 0.20 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
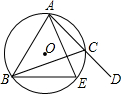 如图,已知四边形ABEC内接于⊙O,点D在AC的延长线上,CE平分∠BCD交⊙O于点E,则下列结论中一定正确的是( )
如图,已知四边形ABEC内接于⊙O,点D在AC的延长线上,CE平分∠BCD交⊙O于点E,则下列结论中一定正确的是( )| A. | AB=AE | B. | AB=BE | C. | AE=BE | D. | AB=AC |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
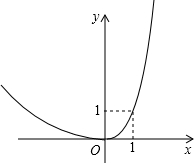 对于某一函数给出如下定义:若存在实数p,当其自变量的值为p时,其函数值等于p,则称p为这个函数的不变值.在函数存在不变值时,该函数的最大不变值与最小不变值之差q称为这个函数的不变长度.特别地,当函数只有一个不变值时,其不变长度q为零.例如,下图中的函数有0,1两个不变值,其不变长度q等于1.
对于某一函数给出如下定义:若存在实数p,当其自变量的值为p时,其函数值等于p,则称p为这个函数的不变值.在函数存在不变值时,该函数的最大不变值与最小不变值之差q称为这个函数的不变长度.特别地,当函数只有一个不变值时,其不变长度q为零.例如,下图中的函数有0,1两个不变值,其不变长度q等于1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com