
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌвбжЊЕу
жаЃЌвбжЊЕу![]() ЃЌЕу
ЃЌЕу![]() дк
дк![]() жсЩЯЃЌвд
жсЩЯЃЌвд![]() ЮЊжБОЖзї
ЮЊжБОЖзї![]() ЃЌЕу
ЃЌЕу![]() дк
дк![]() жсЩЯЃЌЧвдкЕу
жсЩЯЃЌЧвдкЕу![]() ЩЯЗНЃЌЙ§Еу
ЩЯЗНЃЌЙ§Еу![]() зї
зї![]() ЕФЧаЯп
ЕФЧаЯп![]() ЃЌ
ЃЌ![]() ЮЊЧаЕуЃЌШчЙћЕу
ЮЊЧаЕуЃЌШчЙћЕу![]() дкЕквЛЯѓЯоЃЌдђГЦ
дкЕквЛЯѓЯоЃЌдђГЦ![]() ЮЊЕу
ЮЊЕу![]() ЕФРыЕуЃЎР§ШчЃЌЭМ1жаЕФ
ЕФРыЕуЃЎР§ШчЃЌЭМ1жаЕФ![]() ЮЊЕу
ЮЊЕу![]() ЕФвЛИіРыЕуЃЎ
ЕФвЛИіРыЕуЃЎ
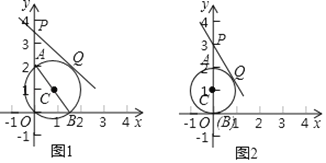
ЃЈ1ЃЉвбжЊЕу![]() ЃЌ
ЃЌ![]() ЮЊ
ЮЊ![]() ЕФРыЕуЃЎ
ЕФРыЕуЃЎ
ЂйШчЭМ2ЃЌШє![]() ЃЌдђдВаФ
ЃЌдђдВаФ![]() ЕФзјБъЮЊ__________ЃЌЯпЖЮ
ЕФзјБъЮЊ__________ЃЌЯпЖЮ![]() ЕФГЄЮЊ__________ЃЛ
ЕФГЄЮЊ__________ЃЛ
ЂкШє![]() ЃЌЧѓЯпЖЮ
ЃЌЧѓЯпЖЮ![]() ЕФГЄЃЛ
ЕФГЄЃЛ
ЃЈ2ЃЉвбжЊ![]() ЃЌжБЯп
ЃЌжБЯп![]() ЃЎ
ЃЎ
ЂйЕБ![]() ЪБЃЌШєжБЯп
ЪБЃЌШєжБЯп![]() ЩЯДцдк
ЩЯДцдк![]() ЕФРыЕу
ЕФРыЕу![]() ЃЌдђЕу
ЃЌдђЕу![]() знзјБъ
знзјБъ![]() ЕФзюДѓжЕЮЊ__________ЃЛ
ЕФзюДѓжЕЮЊ__________ЃЛ
ЂкМЧжБЯп![]() дк
дк![]() ЕФВПЗжЮЊЭМаЮ
ЕФВПЗжЮЊЭМаЮ![]() ЃЌШчЙћЭМаЮ
ЃЌШчЙћЭМаЮ![]() ЩЯДцдк
ЩЯДцдк![]() ЕФРыЕуЃЌжБНгаДГі
ЕФРыЕуЃЌжБНгаДГі![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
ЁОД№АИЁП(1)ЂйЃЈ0ЃЌ1ЃЉЃЛ![]() ЃЛЯъЧщМћНтЮіЃЛЂк
ЃЛЯъЧщМћНтЮіЃЛЂк![]() ЃЌЯъЧщМћНтЮіЃЛЃЈ2ЃЉЂй6ЃЌЯъЧщМћНтЮіЃЛЂкЕБkЃМ0ЪБЃЌ1-2
ЃЌЯъЧщМћНтЮіЃЛЃЈ2ЃЉЂй6ЃЌЯъЧщМћНтЮіЃЛЂкЕБkЃМ0ЪБЃЌ1-2![]() <kЁм
<kЁм![]() ЛђЕБkЃО0ЪБЃЌ
ЛђЕБkЃО0ЪБЃЌ![]() Ёмk<1+2
Ёмk<1+2![]() ЃЛЯъЧщМћНтЮіЃЛ
ЃЛЯъЧщМћНтЮіЃЛ
ЁОНтЮіЁП
ЃЈ1ЃЉЂйШчЭМПЩжЊЃКC(0ЃЌ1)ЃЌдкRt![]() PQCжаЃЌCQ=1ЃЌPC=2ЃЌПЩЕУЯпЖЮ
PQCжаЃЌCQ=1ЃЌPC=2ЃЌПЩЕУЯпЖЮ![]() ЕФГЄЃЛ
ЕФГЄЃЛ
ЂкШчЭМЃЌЙ§CзїCMЁЭyжсгкЕуMЃЌСЌНгCPЃЌCQЃЌM(0ЃЌ1)ЃЌдкRt![]() ACMжаЃЌгЩЙДЙЩЖЈРэПЩЕУCA=
ACMжаЃЌгЩЙДЙЩЖЈРэПЩЕУCA=![]() ЃЌCQ=
ЃЌCQ=![]() ЃЌдкRt
ЃЌдкRt![]() PCMжаЃЌгЩЙДЙЩЖЈРэПЩЕУPC=
PCMжаЃЌгЩЙДЙЩЖЈРэПЩЕУPC=![]() ЃЌдкRt
ЃЌдкRt![]() PCQжаЃЌгЩЙДЙЩЖЈРэПЩЕУPQ=
PCQжаЃЌгЩЙДЙЩЖЈРэПЩЕУPQ=![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЂйЕБk=1ЪБЃЌy=x+4ЃЌQЃЈt-4ЃЌtЃЉЃЌPЕФзнзјБъЮЊ4ЪБЃЌPQгыдВCЯрЧаЃЌЩшBЃЈmЃЌ0ЃЉЃЌдђдВаФЮЊ![]() ЃЌгЩCQЁЭPQЃЌПЩЧѓCQЕФНтЮіЪНЮЊ
ЃЌгЩCQЁЭPQЃЌПЩЧѓCQЕФНтЮіЪНЮЊ![]() ЃЌQЕуКсзјБъЮЊ
ЃЌQЕуКсзјБъЮЊ![]() ЃЌдђCЃЈ2t-5ЃЌ1ЃЉЃЌдйгЩCQ=ACЃЌЕУЕНt=6Лђt=2ЃЛ
ЃЌдђCЃЈ2t-5ЃЌ1ЃЉЃЌдйгЩCQ=ACЃЌЕУЕНt=6Лђt=2ЃЛ
Ђкy=kx+k+3ОЙ§ЖЈЕуЃЈ-1ЃЌ3)ЃЌPQЪЧдВЕФЧаЯпЃЌAOЪЧдВЕФЯвЃЌдђга![]() ЃЌЕБk<0ЪБЃЌQЕуЕФдкЖЫЕуЃЈ-1ЃЌ3ЃЉКЭЃЈ1ЃЌ2k+3ЃЉжЎМфдЫЖЏЃЌЕБPЃЈ0ЃЌ4ЃЉЪБЃЌPQ=2
ЃЌЕБk<0ЪБЃЌQЕуЕФдкЖЫЕуЃЈ-1ЃЌ3ЃЉКЭЃЈ1ЃЌ2k+3ЃЉжЎМфдЫЖЏЃЌЕБPЃЈ0ЃЌ4ЃЉЪБЃЌPQ=2![]() ЃЌ.вдPЮЊдВаФЃЌPQГЄЮЊАыОЖЕФдВгыyжсНЛгкЕуЃЈ0ЃЌ4-2
ЃЌ.вдPЮЊдВаФЃЌPQГЄЮЊАыОЖЕФдВгыyжсНЛгкЕуЃЈ0ЃЌ4-2![]() ЃЉЃЌДЫЪБk=1-2
ЃЉЃЌДЫЪБk=1-2![]() ЃЌЕБPЃЈ0ЃЌ3ЃЉЪБЃЌPQ=
ЃЌЕБPЃЈ0ЃЌ3ЃЉЪБЃЌPQ=![]() ЃЌQЃЈ1ЃЌ2k+3ЃЉЃЌ
ЃЌQЃЈ1ЃЌ2k+3ЃЉЃЌ![]() ЃЌЫљвд1-2
ЃЌЫљвд1-2![]() <kЁм
<kЁм![]() ЃЛЕБk>0ЪБЃЌЕБPЃЈ0ЃЌ4)ЪБЃЌPQ=2
ЃЛЕБk>0ЪБЃЌЕБPЃЈ0ЃЌ4)ЪБЃЌPQ=2![]() ЃЌвдPЮЊдВаФЃЌPQГЄЮЊАыОЖЕФдВгыyжсНЛгкЕуЃЈ0ЃЌ4+2
ЃЌвдPЮЊдВаФЃЌPQГЄЮЊАыОЖЕФдВгыyжсНЛгкЕуЃЈ0ЃЌ4+2![]() ЃЉЃЌДЫЪБk=1+2
ЃЉЃЌДЫЪБk=1+2![]() ЃЌЕБP(0ЃЌ3)ЪБЃЌPQ=
ЃЌЕБP(0ЃЌ3)ЪБЃЌPQ=![]() ЃЌQЃЈ1ЃЌ2k+3ЃЉЃЌ
ЃЌQЃЈ1ЃЌ2k+3ЃЉЃЌ![]() ЃЌ
ЃЌ![]() Ёмk<1+2
Ёмk<1+2![]() ЃЛ
ЃЛ
НтЃК
ЃЈ1ЃЉЂйШчЭМПЩжЊЃКCЃЈ0ЃЌ1ЃЉЃЌ
дкRt![]() PQCжаЃЌCQ=1ЃЌPC=2ЃЌ
PQCжаЃЌCQ=1ЃЌPC=2ЃЌ
Ёр![]() ЃЛ
ЃЛ
ЙЪД№АИЮЊЃКЃЈ0ЃЌ1ЃЉЃЛ![]() ЃЛ
ЃЛ
ЂкШчЭМЃЌЙ§CзїCMЁЭyжсгкЕуMЃЌСЌНгCPЃЌCQЃЌ
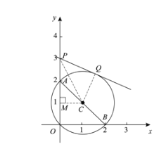
ЁпAЃЈ0ЃЌ2ЃЉЃЌBЃЈ2ЃЌ0ЃЉЃЌ
ЁрCЃЈ1ЃЌ1ЃЉЃЌ
ЁрMЃЈ0ЃЌ1ЃЉЃЌ
дкRt![]() ACMжаЃЌгЩЙДЙЩЖЈРэПЩЕУCA=
ACMжаЃЌгЩЙДЙЩЖЈРэПЩЕУCA=![]() ЃЌ
ЃЌ
ЁрCQ=![]() ЃЌ
ЃЌ
ЁпPЃЈ0ЃЌ3ЃЉЃЌMЃЈ0ЃЌ1ЃЉЃЌ
ЁрPM=2ЃЌ
дкRt![]() PCMжаЃЌгЩЙДЙЩЖЈРэПЩЕУPC=
PCMжаЃЌгЩЙДЙЩЖЈРэПЩЕУPC=![]() ЃЌ
ЃЌ
дкRt![]() PCQжаЃЌгЩЙДЙЩЖЈРэПЩЕУPQ=
PCQжаЃЌгЩЙДЙЩЖЈРэПЩЕУPQ=![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЂйЕБk=1ЪБЃЌy=x+4ЃЌ
ЁрQЃЈt-4ЃЌtЃЉЃЌ
Ёп![]() ЃЌ
ЃЌ
ЁрPЕФзнзјБъЮЊ4ЪБЃЌPQгыдВCЯрЧаЃЌ
ЩшBЃЈmЃЌ0ЃЉЃЌ
ЁрC![]() ЃЌ
ЃЌ
ЁпCQЁЭPQЃЌ
ЁрCQЕФНтЮіЪНЮЊ![]() ЃЌ
ЃЌ
ЁрQЕуКсзјБъЮЊ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёрm=4t-10ЃЌ
ЁрCЃЈ2t-5ЃЌ1ЃЉЃЌ
ЁпCQ=ACЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёрt=6Лђt=2ЃЛ
ЁрtЕФзюДѓжЕЮЊ6ЃЛ
ЙЪД№АИЮЊЃК6.
ЂкЁп-1ЁмxЁм1ЃЌ
Ёпy=kx+k+3ОЙ§ЖЈЕуЃЈ-1ЃЌ3)ЃЌ
ЁпPQЪЧдВЕФЧаЯпЃЌAOЪЧдВЕФЯвЃЌ
Ёр![]() ЃЌ
ЃЌ
ЕБk<0ЪБЃЌQЕуЕФдкЖЫЕуЃЈ-1ЃЌ3ЃЉКЭЃЈ1ЃЌ2k+3ЃЉжЎМфдЫЖЏЃЌ
ЕБPЃЈ0ЃЌ4ЃЉЪБЃЌPQ=2![]() ЃЌ
ЃЌ
.вдPЮЊдВаФЃЌPQГЄЮЊАыОЖЕФдВгыyжсНЛгкЕуЃЈ0ЃЌ4-2![]() ЃЉЃЌ
ЃЉЃЌ
ДЫЪБk=1-2![]() ЃЌ
ЃЌ
ЕБPЃЈ0ЃЌ3ЃЉЪБЃЌPQ=![]() ЃЌQЃЈ1ЃЌ2k+3ЃЉЃЌ
ЃЌQЃЈ1ЃЌ2k+3ЃЉЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
МД1-2![]() <kЁм
<kЁм![]() ЃЛ
ЃЛ
ЕБk>0ЪБЃЌЕБPЃЈ0ЃЌ4)ЪБЃЌPQ=2![]() ЃЌ
ЃЌ
вдPЮЊдВаФЃЌPQГЄЮЊАыОЖЕФдВгыyжсНЛгкЕуЃЈ0ЃЌ4+2![]() ЃЉЃЌ
ЃЉЃЌ
ДЫЪБk=1+2![]() ЃЌ
ЃЌ
ЕБP(0ЃЌ3)ЪБЃЌPQ=![]() ЃЌ
ЃЌ
QЃЈ1ЃЌ2k+3ЃЉЃЌ
![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
МД![]() Ёмk<1+2
Ёмk<1+2![]() ЃЛ
ЃЛ


 ПкЫуЬтПЈМггІгУЬтМЏбЕЯЕСаД№АИ
ПкЫуЬтПЈМггІгУЬтМЏбЕЯЕСаД№АИ злКЯздВтЯЕСаД№АИ
злКЯздВтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
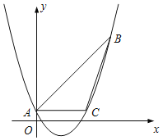
ЁОЬтФПЁПШчЭМЃЌвбжЊХзЮяЯпyЃНax2Љ2x+cОЙ§ЁїABCЕФШ§ИіЖЅЕуЃЌЦфжаЕуA(0ЃЌ1)ЃЌЕуB(9ЃЌ10)ЃЌACЁЮxжсЃЎ
(1)ЧѓетЬѕХзЮяЯпЕФНтЮіЪН.
(2)ЧѓtanЁЯABCЕФжЕ.
(3)ШєЕуDЮЊХзЮяЯпЕФЖЅЕуЃЌЕуEЪЧжБЯпACЩЯвЛЕуЃЌЕБЁїCDEгыЁїABCЯрЫЦЪБЃЌЧѓЕуEЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
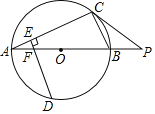
ЁОЬтФПЁПШчЭМЃЌABЮЊЁбOЕФжБОЖЃЌЕуPдкABЕФбгГЄЯпЩЯЃЌЕуCдкЁбOЩЯЃЌЧвPC2ЃНPBPAЃЎ
ЃЈ1ЃЉЧѓжЄЃКPCЪЧЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉвбжЊPCЃН20ЃЌPBЃН10ЃЌЕуDЪЧ![]() ЕФжаЕуЃЌDEЁЭACЃЌДЙзуЮЊEЃЌDEНЛABгкЕуFЃЌЧѓEFЕФГЄЃЎ
ЕФжаЕуЃЌDEЁЭACЃЌДЙзуЮЊEЃЌDEНЛABгкЕуFЃЌЧѓEFЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
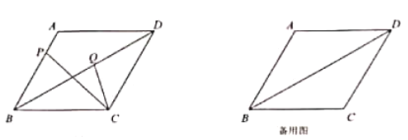
ЁОЬтФПЁПвбжЊдкСтаЮABCDжаЃЌAB=4ЃЌЁЯBAD=120ЁуЃЌЕуPЪЧжБЯпABЩЯШЮвтвЛЕуЃЌСЊНсPCЃЌдкЁЯPCDФкВПзїЩфЯпCQгыЖдНЧЯпBDНЛгкЕуQЃЈгыBЁЂDВЛжиКЯЃЉЃЌЧвЁЯPCQ=30Ёу.
ЃЈ1ЃЉШчЭМЃЌЕБЕуPдкБпABЩЯЪБЃЌШчЙћBP=3ЃЌЧѓЯпЖЮPCЕФГЄЃЛ
ЃЈ2ЃЉЕБЕуPдкЩфЯпBAЩЯЪБЃЌЩш![]() ЃЌЧѓyЙигк
ЃЌЧѓyЙигк![]() ЕФКЏЪ§НтЮіЪНМАЖЈвхгђЃЛ
ЕФКЏЪ§НтЮіЪНМАЖЈвхгђЃЛ
ЃЈ3ЃЉСЊНсPQЃЌжБЯпPQгыжБЯпBCНЛгкЕуEЃЌШчЙћ![]() гы
гы![]() ЯрЫЦЃЌЧѓЯпЖЮBPЕФГЄ.
ЯрЫЦЃЌЧѓЯпЖЮBPЕФГЄ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮ![]() ФкНггкЁб
ФкНггкЁб![]() ЃЌЕу
ЃЌЕу![]() дк
дк![]() ЩЯЃЌ
ЩЯЃЌ![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зїЁб
зїЁб![]() ЕФЧаЯпЃЌЗжБ№НЛ
ЕФЧаЯпЃЌЗжБ№НЛ![]() ЃЌ
ЃЌ![]() ЕФбгГЄЯпгкЕу
ЕФбгГЄЯпгкЕу![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШє![]() ЃЌ
ЃЌ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФГЄЃЎ
ЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
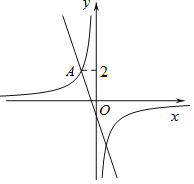
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌжБЯп![]() гыЫЋЧњЯп
гыЫЋЧњЯп![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() ЃЎ
ЃЎ
![]() ЧѓЫЋЧњЯп
ЧѓЫЋЧњЯп![]() ЕФБэДяЪНЃЛ
ЕФБэДяЪНЃЛ
![]() Й§ЖЏЕу
Й§ЖЏЕу![]() ЧвДЙжБгкxжсЕФжБЯпгыжБЯп
ЧвДЙжБгкxжсЕФжБЯпгыжБЯп![]() МАЫЋЧњЯп
МАЫЋЧњЯп![]() ЕФНЛЕуЗжБ№ЮЊBКЭCЃЌЕБЕуBЮЛгкЕуCЯТЗНЪБЃЌЧѓГіnЕФШЁжЕЗЖЮЇЃЎ
ЕФНЛЕуЗжБ№ЮЊBКЭCЃЌЕБЕуBЮЛгкЕуCЯТЗНЪБЃЌЧѓГіnЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
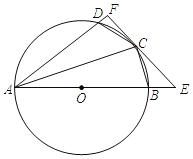
ЁОЬтФПЁПШчЭМЂйЃЌЕШБпШ§НЧаЮ![]() ЕФБпГЄЮЊ2ЃЌ
ЕФБпГЄЮЊ2ЃЌ![]() ЪЧ
ЪЧ![]() БпЩЯЕФШЮвЛЕу(гы
БпЩЯЕФШЮвЛЕу(гы![]() ВЛжиКЯ)ЃЌЩш
ВЛжиКЯ)ЃЌЩш![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌвд
ЃЌвд![]() ЮЊБпЯђСНВрзїЕШБпШ§НЧаЮ
ЮЊБпЯђСНВрзїЕШБпШ§НЧаЮ![]() КЭЕШБпШ§НЧаЮ
КЭЕШБпШ§НЧаЮ![]() ЃЌЗжБ№гыБп
ЃЌЗжБ№гыБп![]() НЛгкЕу
НЛгкЕу![]() ЃЎ
ЃЎ
(1)ЧѓжЄЃК![]() ЃЛ
ЃЛ
(2)ЧѓЫФБпаЮ![]() гыЁїABCжиЕўВПЗжЕФУцЛ§
гыЁїABCжиЕўВПЗжЕФУцЛ§![]() гы
гы![]() жЎМфЕФКЏЪ§ЙиЯЕЪНМА
жЎМфЕФКЏЪ§ЙиЯЕЪНМА![]() ЕФзюаЁжЕЃЛ
ЕФзюаЁжЕЃЛ
(3)ШчЭМЂкЃЌСЌНг![]() ЃЌЗжБ№гыБп
ЃЌЗжБ№гыБп![]() НЛгкЕу
НЛгкЕу![]() ЃЎЕБ
ЃЎЕБ![]() ЮЊКЮжЕЪБЃЌ
ЮЊКЮжЕЪБЃЌ![]() ЃЎ
ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
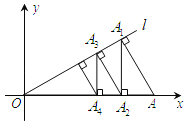
ЁОЬтФПЁПШчЭМЃЌЙ§Еу![]() зїжБЯп
зїжБЯп![]() ЕФДЙЯпЃЌДЙзуЮЊЕу
ЕФДЙЯпЃЌДЙзуЮЊЕу![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() жсЃЌДЙзуЮЊЕу
жсЃЌДЙзуЮЊЕу![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() ЃЌДЙзуЮЊЕу
ЃЌДЙзуЮЊЕу![]() ЁЃЌетбљвРДЮЯТШЅЃЌЕУЕНвЛзщЯпЖЮ
ЁЃЌетбљвРДЮЯТШЅЃЌЕУЕНвЛзщЯпЖЮ![]() ЁЃЌдђЯпЖЮ
ЁЃЌдђЯпЖЮ![]() ЕФГЄЮЊ__________ЃЎ
ЕФГЄЮЊ__________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
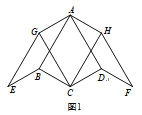
ЁОЬтФПЁПдкЫФБпаЮ ABCDжаЃЌABЃНADЃЌЁЯBADЃН60ЁуЃЌБпBCШЦЕуBЫГЪБеыа§зЊ120ЁуЕУЕНBEЃЌБпDCШЦЕуDФцЪБеыа§зЊ120ЁуЕУЕНDFЃЌЫФБпаЮABEGКЭЫФБпаЮADFHЮЊЦНааЫФБпаЮЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌШєBCЃНCDЃЌЁЯBCDЃН120ЁуЃЌдђЁЯGCHЃН_______ЁуЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌШєBCЁйCDЃЌЬНОПЁЯGCHЕФДѓаЁЪЧЗёЗЂЩњБфЛЏЃЌВЂжЄУїФуЕФНсТлЃЛ
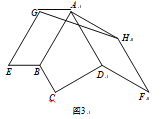
ЃЈ3ЃЉШчЭМ3ЃЌШєЁЯBCDЃНЁЯADCЃН90ЁуЃЌABЃН![]() ЧыжБНгаДГіЁїAGHЕФжмГЄЃЎ
ЧыжБНгаДГіЁїAGHЕФжмГЄЃЎ

ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com