
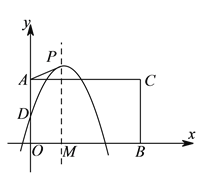
【题目】如图,在平面直角坐标系中,点![]() ,
, ![]() 分别是
分别是![]() 轴正半轴,
轴正半轴, ![]() 轴正半轴上两动点,
轴正半轴上两动点, ![]() ,
, ![]() ,以
,以![]() ,
, ![]() 为邻边构造矩形
为邻边构造矩形![]() ,抛物线
,抛物线![]() 交
交![]() 轴于点
轴于点![]() ,
, ![]() 为顶点,
为顶点, ![]() 轴于点
轴于点![]() .
.
(![]() )求
)求![]() ,
, ![]() 的长(结果均用含
的长(结果均用含![]() 的代数式表示);
的代数式表示);
(![]() )当
)当![]() 时,求该抛物线的表达式;
时,求该抛物线的表达式;
(![]() )在点
)在点![]() 在整个运动过程中,若存在
在整个运动过程中,若存在![]() 是等腰三角形,请求出所有满足条件的
是等腰三角形,请求出所有满足条件的![]() 的值.
的值.
【答案】(1)![]() ,
, ![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]() 或
或![]()
【解析】试题分析:(1)点D在y=-![]() x2+3x+k上,且在y轴上,即y=0求出点D坐标,根据抛物线顶点公式,求出即可;
x2+3x+k上,且在y轴上,即y=0求出点D坐标,根据抛物线顶点公式,求出即可;
(2)先用k表示出相关的点的坐标,根据PM=BM建立方程即可;
(3)先用k表示出相关的点的坐标,根据△ADP是等腰三角形,分三种情况,AD=AP,DA=DP,PA=PD计算.
试题解析:( ![]() )把
)把![]() 代入
代入![]() ,
, ![]() ,
,
∴![]() ,
,
∵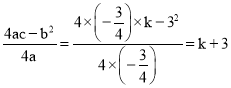 ,
,
∴![]() .
.
(![]() )∵
)∵ ,
,
∴![]() ,
, ![]() ,
,
又∵![]() ,
, ![]() ,
,
∴![]() ,
,
∴![]() ,
,
抛物线表达式为![]() .
.
(![]() )当
)当![]() 在矩形
在矩形![]() 外时,
外时,
如图![]() ,过
,过![]() 作
作![]() 于
于![]() 点,
点,
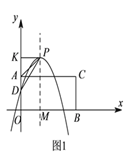
当![]() 时,
时,
∵![]() ,
,
∴![]() ,
,
![]() ,
,
![]() ,
,
在![]() 中,
中, ![]() ,
,
∴![]() ,
,
∴![]() ,
,
当![]() 在矩形
在矩形![]() 内部时,
内部时,
![]() 时,如图
时,如图![]() ,过
,过![]() 作
作![]() 于
于![]() ,
,
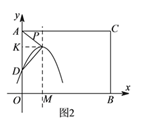
![]() ,
, ![]() ,
,
![]() ,
,
又∵![]() ,
,
∴![]() ,∴
,∴![]() ,
,
当![]() 时,如图3,过
时,如图3,过![]() 作
作![]() 于
于![]() ,
,
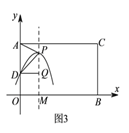
![]() ,
,
![]() ,
, ![]() ,
,
在![]() 中,
中, ![]() ,
,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系第一象限中,已知点![]() 坐标为
坐标为![]() ,点
,点![]() 坐标为
坐标为![]() ,点
,点![]() 坐标为
坐标为![]() ,动点
,动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度匀速向点
个单位长度的速度匀速向点![]() 方向运动,与此同时,
方向运动,与此同时,![]() 轴上动点
轴上动点![]() 从点
从点![]() 出发,以相同的速度向右运动, 两动点运动时间为:
出发,以相同的速度向右运动, 两动点运动时间为:![]() , 以
, 以![]() 分别为边作矩形
分别为边作矩形![]() , 过点
, 过点![]() 作双曲线交线段
作双曲线交线段![]() 于点
于点![]() ,作
,作![]() 中点
中点![]() ,连接
,连接![]()
(1)当![]() 时,求点
时,求点![]() 的坐标.
的坐标.
(2)若![]() 平分
平分![]() , 则
, 则![]() 的值为多少?
的值为多少?
(3)若![]() 为直角, 则
为直角, 则![]() 的值为多少?
的值为多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在东营市中小学标准化建设工程中,某学校计划购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元.
(1)求每台电脑、每台电子白板各多少万元?
(2)根据学校实际,需购进电脑和电子白板共30台,总费用不超过30万元,但不低于28万元,请你通过计算求出有几种购买方案,哪种方案费用最低.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校数学兴趣小组利用自制的直角三角形硬纸板DEF来测量操场旗杆AB的高度,他们通过调整测量位置,使斜边DF与地面保持平行,并使边DE与旗杆顶点A在同一直线上,已知DE=0.5米,EF=0.25米,目测点D到地面的距离DG=1.5米,到旗杆的水平距离DC=20米,求旗杆的高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
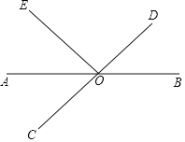
【题目】如图,直线AB,CD相交于点O,OA平分∠EOC.
(1)若∠EOC=80°,求∠BOD的度数;
(2)若∠EOC=∠EOD,求∠BOD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某旅行社的一则广告如下:我社推出去井冈山红色旅游,收费标准为:如果组团人数不超过30人,人均收费800元;如果人数多于30人,那么每增加1人,人均收费降低10元,但人均收费不得低于500元,甲公司想分批组织员工到井冈山红色旅游学习.
(1)如果第一批组织38人去学习,则公司应向旅行社交费 元;
(2)如果公司计划用29250元组织第一批员工去学习,问这次旅游学习应安排多少人参加?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,BD的垂直平分线交AD于E,交BC于F,连接BE 、DF.

(1)判断四边形BEDF的形状,并说明理由;
(2)若AB=8,AD=16,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
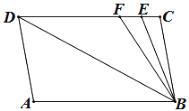
【题目】如图,已知直线AB∥CD,∠A=∠C=100°,E、F在CD上,且满足∠DBF=∠ABD,BE平分∠CBF.
(1)直线AD与BC有何位置关系?请说明理由.
(2)求∠DBE的度数.
(3)若把AD左右平行移动,在平行移动AD的过程中,是否存在某种情况,使∠BEC=∠ADB?若存在,求出此时∠ADB的度数;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com