
”¾ĢāÄæ”抔ÕŵŚŅ»“ĪÓĆ180ŌŖ¹ŗĀņĮĖ8Ģ׶łĶÆ·ž×°£¬ŅŌŅ»¶Ø¼Ūøń³öŹŪ.Čē¹ūŅŌĆæĢ׶łĶÆ·ž×°80ŌŖµÄ¼ŪøńĪŖ±ź×¼£¬³¬³öµÄ¼Ē×÷ÕūŹż£¬²»×ćµÄ¼Ē×÷øŗŹż£¬¼ĒĀ¼ČēĻĀ£Øµ„Ī»£ŗŌŖ£©£ŗ
![]()
ĒėĶعż¼ĘĖćĖµĆ÷£ŗ
£Ø1£©Š”ÕÅĀōĶźÕā8Ģ׶łĶÆ·ž×°ŗóŹĒÓÆĄū»¹ŹĒæ÷Ėš£æÓÆĄū£Ø»ņæ÷Ėš£©ĮĖ¶ąÉŁĒ®£æ
£Ø2£©ĆæĢ׶łĶÆ·ž×°µÄĘ½¾łŹŪ¼ŪŹĒ¶ąÉŁŌŖ£æ
£Ø3£©Š”ÕŵŚ¶ž“ĪÓƵŚŅ»“ĪµÄ½ų¼ŪŌŁ“Ī¹ŗĀņ900ŌŖµÄ¶łĶÆ·ž×°£¬Čē¹ūĖūŌ¤¼ĘµŚ¶ž“ĪĆæĢ×·ž×°µÄĘ½¾łŹŪ¼Ū75ŌŖ£¬°“ĖūµÄŌ¤¼ĘµŚ¶ž“ĪŹŪ¼ŪæÉ»ńĄū¶ąÉŁŌŖ£æ
”¾“š°ø”æ£Ø1£©µ±ĖūĀōĶźÕā°ĖĢ׶łĶÆ·ž×°ŗóŹĒÓÆĄūĮĖ£¬ÓÆĄūĮĖ![]() ŌŖ£»£Ø2£©ĆæĢ׶łĶÆ·ž×°µÄĘ½¾łŹŪ¼ŪŹĒ
ŌŖ£»£Ø2£©ĆæĢ׶łĶÆ·ž×°µÄĘ½¾łŹŪ¼ŪŹĒ![]() ŌŖ£»£Ø3£©°“ĖūµÄŌ¤¼ĘµŚ¶ž“ĪŹŪ¼ŪæÉ»ńĄū
ŌŖ£»£Ø3£©°“ĖūµÄŌ¤¼ĘµŚ¶ž“ĪŹŪ¼ŪæÉ»ńĄū![]() ŌŖ.
ŌŖ.
”¾½āĪö”æ
£Ø1£©°ŃĖłµĆµÄÕżøŗŹżĻą¼Ó£¬ŌŁĶ¬ŅŌ55ŌŖŹŪ¼ŪŹŪ³öµÄ×ܼŪĻą¼Ó£¬Ēó³öĀņ³öµÄĒ®Źż£¬ŌŁĶ¬400ŌŖ½ųŠŠ±Č½Ļ£¬æÉÖŖ׬ĮĖ»¹ŹĒæ÷ĮĖ£¬½ų¶ųĒó³ö׬»ņæ÷µÄĒ®Źż£»
£Ø2£©ÓĆŹŪ³öµÄ×ܼŪ³żŅŌ8æÉĒó³öĘ½¾łŹŪ¼ŪŹĒ¶ąÉŁŌŖ£¬¾Ż“Ė½ā“š£®
£Ø3£©øł¾ŻĄūČó=ŹŪ¼Ū-½ų¼Ū¼“æÉĒóµĆ.
(1)(+12)+(13)+(+15)+(+11)+(17)+(-11)+0+(13)= 16.
80”Į8 16=64016=624(ŌŖ)
624>180£¬ĖłŅŌ׬Ē®
624180=444(ŌŖ)
“š£ŗµ±ĖūĀōĶźÕā°ĖĢ׶łĶÆ·ž×°ŗóŹĒÓÆĄūĮĖ£¬ÓÆĄūĮĖ![]() ŌŖ£»
ŌŖ£»
(2)624”Ā8=78(ŌŖ)
“š£ŗĆæĢ׶łĶÆ·ž×°µÄĘ½¾łŹŪ¼ŪŹĒ78ŌŖ.
(3)ĆæĢ×ŅĀ·žµÄ½ų¼ŪĪŖ£ŗ180”Ā8=22.5ŌŖ,
µŚ¶ž“ĪæÉŅŌ¹ŗ½ų·ž×°900”Ā22.5=40Ģ×£¬
![]()
“š£ŗ°“ĖūµÄŌ¤¼ĘµŚ¶ž“ĪŹŪ¼ŪæÉ»ńĄū![]() ŌŖ.
ŌŖ.



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÖ±Ļßy=©xÓėĖ«ĒśĻßy=![]() ŌŚĶ¬Ņ»×ų±źĻµÖŠµÄ“óÖĀĪ»ÖĆŹĒ£Ø””””£©
ŌŚĶ¬Ņ»×ų±źĻµÖŠµÄ“óÖĀĪ»ÖĆŹĒ£Ø””””£©
A.
B.
C.
D.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖa£¬b£¬cĪŖ·ĒĮćµÄŹµŹż£¬Ōņ![]() µÄæÉÄÜÖµµÄøöŹżĪŖ£Ø””””£©
µÄæÉÄÜÖµµÄøöŹżĪŖ£Ø””””£©
A. 4 B. 5 C. 6 D. 7
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ÓŠŅ»øöæÉŅŌ×ŌÓÉ×Ŗ¶ÆµÄ×ŖÅĢ±»Ę½¾ł·Ö³É3øöÉČŠĪ£¬·Ö±š±źÓŠ1”¢2”¢3ČżøöŹż×Ö£¬Š”ĶõŗĶŠ”Ąīø÷×Ŗ¶ÆŅ»“Ī×ŖÅĢĪŖŅ»“ĪÓĪĻ·£¬µ±Ćæ“Ī×ŖÅĢĶ£Ö¹ŗó£¬ÖøÕėĖłÖøÉČŠĪÄŚµÄŹżĪŖø÷×ŌĖłµĆµÄŹż£¬Ņ»“ĪÓĪĻ·½įŹųµĆµ½Ņ»×鏿£ØČōÖøÕėÖøŌŚ·Ö½ēĻߏ±ÖŲ×Ŗ£©£®
£Ø1£©ĒėÄćÓĆŹ÷דĶ¼»ņĮŠ±ķµÄ·½·Ø±ķŹ¾³öĆæ“ĪÓĪĻ·æÉÄܳöĻÖµÄĖłÓŠ½į¹ū£»
£Ø2£©ĒóĆæ“ĪÓĪĻ·½įŹųµĆµ½µÄŅ»×鏿Ē”ŗĆŹĒ·½³Ģx2©3x+2=0µÄ½āµÄøÅĀŹ£®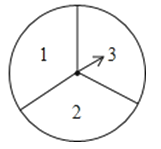
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼1£¬½«Ņ»Õų¤·½ŠĪµÄÖ½¶ŌÕŪŅ»“Ī£¬Č»ŗóŃŲÕŪŗŪ¼ōæŖ£¬æÉŅŌ½«ÕāÕÅÖ½·ÖĪŖĮ½²æ·Ö£ŗČēĶ¼2£¬Čē¹ū¶ŌÕŪĮ½“Ī£¬Č»ŗóŃŲ×īŗóŅ»“ĪµÄÕŪŗŪ¼ōæŖ£¬æÉŅŌ½«ÕāÕÅÖ½·ÖĪŖČż²æ·Ö£»ÓĆĶ¬ŃłµÄ²Ł×÷·½·Ø¼ĢŠųĻĀČ„£¬Čē¹ū¶ŌÕŪ4“Ī£¬Č»ŗóŃŲ×īŗóŅ»“ĪµÄÕŪŗŪ¼ōæŖ£¬ŌņæÉŅŌ½«Ėü¼ō³É_______²æ·Ö£»Čē¹ū¶ŌÕŪ![]() “Ī£¬ŃŲ×īŗóŅ»“ĪµÄÕŪŗŪ¼ōæŖ£¬ŌņæÉŅŌ½«Ėü¼ō³É_______ ²æ·Ö.£Ø×īŗóŅ»æÕÓĆŗ¬
“Ī£¬ŃŲ×īŗóŅ»“ĪµÄÕŪŗŪ¼ōæŖ£¬ŌņæÉŅŌ½«Ėü¼ō³É_______ ²æ·Ö.£Ø×īŗóŅ»æÕÓĆŗ¬![]() µÄŹ½×Ó±ķŹ¾£©
µÄŹ½×Ó±ķŹ¾£©


£ØĶ¼1£© £ØĶ¼2£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijŹŠĪŖ»ŗ½ā³ĒŹŠ½»ĶØŃ¹Į¦£¬¾ö¶ØŠŽ½ØČĖŠŠĢģĒÅ£¬ŌÉč¼ĘĢģĒŵÄĀ„ĢŻ³¤AB=6m£¬”ĻABC=45”ć£¬ŗóæ¼ĀĒµ½°²Č«ŅņĖŲ£¬½«Ā„ĢŻ½ÅBŅʵ½CBŃÓ³¤ĻßÉĻµćD“¦£¬Ź¹”ĻADC=30”ć£ØČēĶ¼ĖłŹ¾£©£®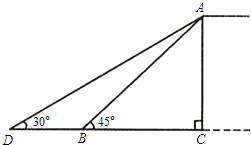
£Ø½į¹ū±£ĮōøłŗÅ£©
£Ø1£©Ēóµ÷ÕūŗóĀ„ĢŻADµÄ³¤£»
£Ø2£©ĒóBDµÄ³¤£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æij×ŌŠŠ³µ³§Ņ»ÖÜ¼Ę»®ĆæČÕÉś²ś![]() Į¾×ŌŠŠ³µ£¬ÓÉÓŚČĖŹżŗĶ²Ł×÷ŌŅņ£¬ĆæČÕŹµ¼ŹÉś²śĮæ·Ö±šĪŖ
Į¾×ŌŠŠ³µ£¬ÓÉÓŚČĖŹżŗĶ²Ł×÷ŌŅņ£¬ĆæČÕŹµ¼ŹÉś²śĮæ·Ö±šĪŖ![]() Į¾”¢
Į¾”¢![]() Į¾”¢
Į¾”¢![]() Į¾”¢
Į¾”¢![]() Į¾”¢
Į¾”¢![]() Į¾”¢
Į¾”¢![]() Į¾”¢
Į¾”¢![]() Į¾£®
Į¾£®
![]() ÓĆÕżøŗŹż±ķŹ¾ĆæČÕŹµ¼ŹÉś²śĮæÓė¼Ę»®ĮæµÄŌö¼õĒéæö£»
ÓĆÕżøŗŹż±ķŹ¾ĆæČÕŹµ¼ŹÉś²śĮæÓė¼Ę»®ĮæµÄŌö¼õĒéæö£»
![]() øĆ³µ³§±¾ÖÜŹµ¼Ź¹²Éś²ś¶ąÉŁĮ¾×ŌŠŠ³µ£æĘ½¾łĆæČÕŹµ¼ŹÉś²ś¶ąÉŁĮ¾×ŌŠŠ³µ£æ
øĆ³µ³§±¾ÖÜŹµ¼Ź¹²Éś²ś¶ąÉŁĮ¾×ŌŠŠ³µ£æĘ½¾łĆæČÕŹµ¼ŹÉś²ś¶ąÉŁĮ¾×ŌŠŠ³µ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÕż·½ŠĪABCDµÄ±ß³¤ĪŖ4£¬½«“ĖÕż·½ŠĪÖĆÓŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Ź¹AB±ßĀäŌŚXÖįµÄÕż°ėÖįÉĻ£¬ĒŅAµćµÄ×ų±źŹĒ£Ø1£¬0£©£®
£Ø1£©Ö±Ļß![]() ¾¹żµćC£¬ĒŅÓėxÖį½»ÓėµćE£¬ĒóĖıߊĪAECDµÄĆ껿£»
¾¹żµćC£¬ĒŅÓėxÖį½»ÓėµćE£¬ĒóĖıߊĪAECDµÄĆ껿£»
£Ø2£©ČōÖ±Ļßl¾¹żµćE£¬ĒŅ½«Õż·½ŠĪABCD·Ö³ÉĆ껿ĻąµČµÄĮ½²æ·Ö£¬ĒóÖ±ĻßlµÄ½āĪöŹ½£»
£Ø3£©ČōÖ±Ļßl1¾¹żµćF£Ø©![]() £¬0£©£¬ĒŅÓėÖ±Ļßy=3xĘ½ŠŠ£¬½«£Ø2£©ÖŠÖ±ĻßlŃŲ×ÅyÖįĻņÉĻĘ½ŅĘ
£¬0£©£¬ĒŅÓėÖ±Ļßy=3xĘ½ŠŠ£¬½«£Ø2£©ÖŠÖ±ĻßlŃŲ×ÅyÖįĻņÉĻĘ½ŅĘ![]() øöµ„Ī»½»ÖįxÓŚµćM£¬½»Ö±Ļßl1ÓŚµćN£¬Ēó”÷NMFµÄĆ껿£®
øöµ„Ī»½»ÖįxÓŚµćM£¬½»Ö±Ļßl1ÓŚµćN£¬Ēó”÷NMFµÄĆ껿£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĪŅĆĒÖŖµĄ£¬¾¹żŌµćµÄÅ×ĪļĻߵĽāĪöŹ½æÉŅŌŹĒy=ax2+bx£Øa”Ł0£©
£Ø1£©¶ŌÓŚÕāŃłµÄÅ×ĪļĻߣŗ
µ±¶„µć×ų±źĪŖ£Ø1£¬1£©Ź±£¬a=£»
µ±¶„µć×ų±źĪŖ£Øm£¬m£©£¬m”Ł0Ź±£¬aÓėmÖ®¼äµÄ¹ŲĻµŹ½ŹĒ
£Ø2£©¼ĢŠųĢ½¾æ£¬Čē¹ūb”Ł0£¬ĒŅ¹żŌµćµÄÅ×ĪļĻ߶„µćŌŚÖ±Ļßy=kx£Øk”Ł0£©ÉĻ£¬ĒėÓĆŗ¬kµÄ“śŹżŹ½±ķŹ¾b£»
£Ø3£©ĻÖÓŠŅ»×é¹żŌµćµÄÅ×ĪļĻߣ¬¶„µćA1 £¬ A2 £¬ ”£¬AnŌŚÖ±Ļßy=xÉĻ£¬ŗį×ų±źŅĄ“ĪĪŖ1£¬2£¬”£¬n£ØĪŖÕżÕūŹż£¬ĒŅn”Ü12£©£¬·Ö±š¹żĆæøö¶„µć×÷xÖįµÄ“¹Ļߣ¬“¹×ć¼ĒĪŖB1 £¬ B2 £¬ ”£¬Bn £¬ ŅŌĻ߶ĪAnBnĪŖ±ßĻņÓŅ×÷Õż·½ŠĪAnBnCnDn £¬ ČōÕā×éÅ×ĪļĻßÖŠÓŠŅ»Ģõ¾¹żDn £¬ ĒóĖłÓŠĀś×ćĢõ¼žµÄÕż·½ŠĪ±ß³¤£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com