
【题目】如图,在等腰直角三角形![]() 中,
中,![]() ,点
,点![]() 为
为![]() 中点,点
中点,点![]() 为外
为外![]() 一点,已知
一点,已知![]() ,则CD的长为( )
,则CD的长为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
过点B作BF⊥CE交CE的延长线于点F,由∠BEC=135°,得∠BEF=45°,再通过解直角三角形BEF求得BF、EF的长,进而可求得BC长,在等腰直角三角形![]() 中,再通过解直角三角形求得AB长,最后利用斜边上的中线等于斜边一半求得CD长即可.
中,再通过解直角三角形求得AB长,最后利用斜边上的中线等于斜边一半求得CD长即可.
解:如图,过点B作BF⊥CE交CE的延长线于点F,
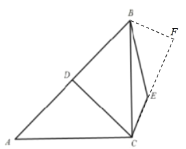
∵∠BEC=135°,
∴∠BEF=180°-135°=45°,
在Rt△BEF中,sin∠BEF=![]() ,cos∠BEF=
,cos∠BEF=![]() ,
,
∴BF=BE·sin∠BEF=![]() ,EF=BE·cos∠BEF=
,EF=BE·cos∠BEF=![]() ,
,
又∵EC=![]() ,
,
∴CF=EC+EF=2![]() ,
,
在Rt△BEF中,BC2=BF2+CF2,
则BC=![]() ,
,
∵在等腰直角三角形![]() 中,∠A=45°,sinA=
中,∠A=45°,sinA=![]() ,
,
∴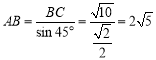 ,
,
∵在直角三角形![]() 中,点
中,点![]() 为
为![]() 中点,
中点,
∴CD=![]() AB=
AB=![]() ,
,
故选:A.


科目:初中数学 来源: 题型:
【题目】在抗击新型冠状病毒感染的肺炎疫情过程中,某医药研究所正在试研发一种抑制新型冠状病毒的药物,据临床观察:如果成人按规定的剂量注射这种药物,注射药物后每毫升血液中的含药量![]() (微克)与时间
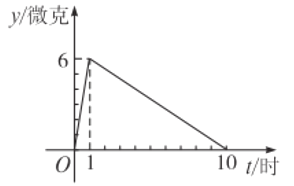
(微克)与时间![]() (小时)之间的关系近似地满足图中折线.
(小时)之间的关系近似地满足图中折线.
(1)求注射药物后每毫升血液中含药量![]() 与时间
与时间![]() 之间的函数关系式,并写出自变量的取值范围;
之间的函数关系式,并写出自变量的取值范围;
(2)据临床观察:每毫升血液中含药量不少于![]() 微克时,对控制病情是有效的.如果病人按规定的剂量注射 该药物后,求控制病情的有效时间.
微克时,对控制病情是有效的.如果病人按规定的剂量注射 该药物后,求控制病情的有效时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校数学兴趣小组的同学测量一架无人飞机P的高度,如图,A,B两个观测点相距![]() ,在A处测得P在北偏东71°方向上,同时在B处测得P在北偏东35°方向上.求无人飞机P离地面的高度.(结果精确到1米,参考数据:
,在A处测得P在北偏东71°方向上,同时在B处测得P在北偏东35°方向上.求无人飞机P离地面的高度.(结果精确到1米,参考数据:![]() ,
,![]() ,sin71°≈0.95,tan71°≈2.90)
,sin71°≈0.95,tan71°≈2.90)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(3,m),B(﹣2,﹣3)是直线AB和某反比例函数的图象的两个交点.
(1)求直线AB和反比例函数的解析式;
(2)观察图象,直接写出当x满足什么范围时,直线AB在双曲线的下方;
(3)反比例函数的图象上是否存在点C,使得△OBC的面积等于△OAB的面积?如果不存在,说明理由;如果存在,求出满足条件的所有点C的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五一期间,甲、乙两人在附近的景点游玩,甲从![]() 两个景点中任意选择一个游玩,乙从
两个景点中任意选择一个游玩,乙从![]() 三个景点中任意选择一个游玩.
三个景点中任意选择一个游玩.
(1)乙恰好游玩![]() 景点的概率为 .
景点的概率为 .
(2)用列表或画树状图的方法列出甲、乙恰好游玩同一景点的所有等可能的结果.并求甲、乙恰好游玩同一景点的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,四边形![]() 内接于⊙
内接于⊙![]() ,
,![]() 是⊙
是⊙![]() 的直径,过点
的直径,过点![]() 的切线与
的切线与![]() 的延长线相交于点
的延长线相交于点![]() .且
.且![]() ,连接
,连接![]() .
.

(1)求证:![]() ;
;
(2)过点![]() 作
作![]() ,垂足为
,垂足为![]() ,当
,当![]() 时,求⊙
时,求⊙![]() 的半径;
的半径;
(3)在(2)的条件下,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形ABCD在第一象限内,边BC与x轴平行,A,B两点的纵坐标分别为4,2,反比例函数y![]() (x>0)的图象经过A,B两点,若菱形ABCD的面积为2
(x>0)的图象经过A,B两点,若菱形ABCD的面积为2![]() ,则k的值为( )
,则k的值为( )
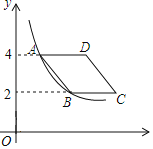
A. 2B. 3C. 4D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个圆形转盘,分黑色、白色两个区域.
(1)某人转动转盘,对指针落在黑色区域或白色区域进行了大量试验,得到数据如下表:
实验次数 | 10 | 100 | 2000 | 5000 | 10000 | 50000 | 100000 |
白色区域次数 | 3 | 34 | 680 | 1600 | 3405 | 16500 | 33000 |
落在白色区域频率 | 0.3 | 0.34 | 0.34 | 0.32 | 0.34 | 0.33 | 0.33 |
请你利用上述实验,估计转动该转盘指针落在白色区域的概率为___________.(精确到0.01);
(2)若该圆形转盘白色扇形的圆心角为120度,黑色扇形的圆心角为![]() ,转动转盘两次,求指针一次落在白色区域,另一次落在黑色区域的概率.
,转动转盘两次,求指针一次落在白色区域,另一次落在黑色区域的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=x2+(2m﹣1)x﹣2m(m>0.5)的最低点的纵坐标为﹣4.
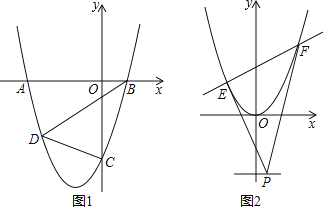
(1)求抛物线的解析式;
(2)如图1,抛物线与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,D为抛物线上的一点,BD平分四边形ABCD的面积,求点D的坐标;
(3)如图2,平移抛物线y=x2+(2m﹣1)x﹣2m,使其顶点为坐标原点,直线y=﹣2上有一动点P,过点P作两条直线,分别与抛物线有唯一的公共点E、F(直线PE、PF不与y轴平行),求证:直线EF恒过某一定点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com