
����Ŀ����ͼ1������ԭ��O��������![]() ��a��0����x�ύ����һ��A��
��a��0����x�ύ����һ��A��![]() ��0�����ڵ�һ��������ֱ��y=x���ڵ�B��2��t����
��0�����ڵ�һ��������ֱ��y=x���ڵ�B��2��t����
��1�������������ߵı���ʽ��
��2���ڵ��������ڵ�����������һ��C��������B��O��CΪ����������ε����Ϊ2�����C�����ꣻ
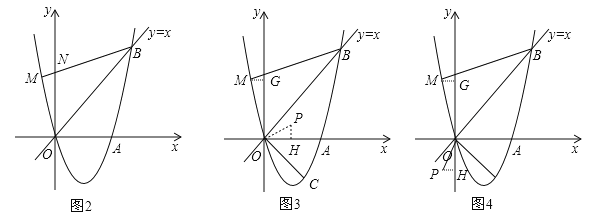
��3����ͼ2������M�������������ϣ�����MBO=��ABO���ڣ�2���������£��Ƿ���ڵ�P��ʹ����POC�ס�MOB�������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�

���𰸡���1��![]() ����2��C��1����1������3��������P������Ϊ��
����2��C��1����1������3��������P��������![]() ��
��![]() ����
����![]() ��
��![]() ����
����
��������
�����������1����ֱ�߽���ʽ�����B�����꣬��A��B���꣬���ô���ϵ��������������ߵı���ʽ��
��2����C��CD��y�ᣬ��x���ڵ�E����OB�ڵ�D����B��BF��CD�ڵ�F�������C�����꣬����C������ɱ�ʾ��CD�ij����Ӷ��ɱ�ʾ����BOC��������������ɵõ�����C������ķ��̣������C�����ꣻ
��3����MB��y���ڵ�N�����֤����ABO�ա�NBO�������N�����꣬�����ֱ��BN�Ľ���ʽ������ֱ��BM�������߽���ʽ�����M�����꣬��M��MG��y���ڵ�G����B��C����������OB��OC�ij��������������ε����ʿ����![]() ��ֵ������P�ڵ�һ������ʱ����P��PH��x���ڵ�H����������֤����MOG�ס�POH����
��ֵ������P�ڵ�һ������ʱ����P��PH��x���ڵ�H����������֤����MOG�ס�POH����![]() =
=![]() =
=![]() ��ֵ�������PH��OH�������P�����ꣻ��P���ڵ�������ʱ��ͬ�������P�����꣮
��ֵ�������PH��OH�������P�����ꣻ��P���ڵ�������ʱ��ͬ�������P�����꣮
���������
��1����B��2��t����ֱ��y=x�ϣ���t=2����B��2��2������A��B����������������߽���ʽ�ɵ���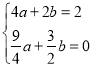 �������
�������![]() ���������߽���ʽΪ
���������߽���ʽΪ![]() ��
��
��2����ͼ1����C��CD��y�ᣬ��x���ڵ�E����OB�ڵ�D����B��BF��CD�ڵ�F������C���������ϵ������ĵ㣬������C��t��2t2��3t������E��t��0����D��t��t������OE=t��BF=2��t��CD=t����2t2��3t��=��2t2+4t����S��OBC=S��CDO+S��CDB=![]() CDOE+
CDOE+![]() CDBF=
CDBF=![]() ����2t2+4t����t+2��t��=��2t2+4t���ߡ�OBC�����Ϊ2������2t2+4t=2�����t1=t2=1����C��1����1����
����2t2+4t����t+2��t��=��2t2+4t���ߡ�OBC�����Ϊ2������2t2+4t=2�����t1=t2=1����C��1����1����

��3�����ڣ���MB��y���ڵ�N����ͼ2����B��2��2�������AOB=��NOB=45�㣬����AOB����NOB�����ߡ�AOB=��NOB��OB=OB����ABO=��NBO�����AOB�ա�NOB��ASA������ON=OA=![]() ����N��0��
����N��0��![]() ����������ֱ��BN����ʽΪy=kx+
����������ֱ��BN����ʽΪy=kx+![]() ����B���������ɵ�2=2k+
����B���������ɵ�2=2k+![]() �����k=
�����k=![]() ����ֱ��BN�Ľ���ʽΪ
����ֱ��BN�Ľ���ʽΪ![]() ������ֱ��BN�������߽���ʽ�ɵ���
������ֱ��BN�������߽���ʽ�ɵ���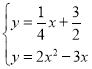 �������
�������![]() ��
��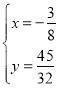 ����M��
����M��![]() ��
��![]() ������C��1����1�������COA=��AOB=45�㣬��B��2��2������OB=
������C��1����1�������COA=��AOB=45�㣬��B��2��2������OB=![]() ��OC=
��OC=![]() ���ߡ�POC�ס�MOB����
���ߡ�POC�ס�MOB����![]() =
=![]() =2����POC=��BOM������P�ڵ�һ����ʱ����ͼ3����M��MG��y���ڵ�G����P��PH��x���ڵ�H����ͼ3
=2����POC=��BOM������P�ڵ�һ����ʱ����ͼ3����M��MG��y���ڵ�G����P��PH��x���ڵ�H����ͼ3
�ߡ�COA=��BOG=45�㣬���MOG=��POH������PHO=��MGO�����MOG�ס�POH����![]() =
=![]() =
=![]() =2����M��
=2����M��![]() ��
��![]() ������MG=
������MG=![]() ��OG=
��OG=![]() ����PH=
����PH=![]() MG=
MG=![]() ��OH=
��OH=![]() OG=
OG=![]() ����P��
����P��![]() ��
��![]() ����
����
����P�ڵ�������ʱ����ͼ4����M��MG��y���ڵ�G����P��PH��y���ڵ�H��ͬ�������PH=![]() MG=
MG=![]() ��OH=
��OH=![]() OG=
OG=![]() ����P����
����P����![]() ��
��![]() ����
����
���Ͽ�֪���������������ĵ�P��������Ϊ��![]() ��
��![]() ����
����![]() ��
��![]() ����
����


 ��Уͨ��֤��Ч��ҵϵ�д�
��Уͨ��֤��Ч��ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����Rt��ABC�У���C=90����AB=5cm��AC=3cm������P�ӵ�B����������BC��1cm/s���ٶ��ƶ������˶���ʱ��Ϊt�룮

��1����BC�ߵij���
��2������ABPΪֱ��������ʱ����t��ֵ��
��3������ABPΪ����������ʱ����t��ֵ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУ�γ̰����У�����ÿ������ֻ�������ڿΣ�
��1����һ��1�������ڶ����簲������ѧ��Ӣ�����θ�һ�ڣ�ͨ������״ͼ�������ѧ�ΰ��������һ�ڵĸ��ʣ�
��2�����������磬������1���ల������ѧ�����������οθ�һ�ڣ�������2���ల������ѧ�����ġ������θ�һ�ڣ���ʱ���������ڿε�ÿһ�ֿα��ŷ����ֵĸ�����![]() ����֪�����������ѧ�ζ���ͬһ����ʦ���Σ���������������λ��ʦ���Σ�������������ѧ�β����ͻ�ĸ��ʣ�
����֪�����������ѧ�ζ���ͬһ����ʦ���Σ���������������λ��ʦ���Σ�������������ѧ�β����ͻ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��![]()
(1) ��ͼ1����BD=DC����C��AE�Ĵ�ֱƽ�����ϡ�AB+BD��DE��ʲô��ϵ�������֤����
(2) ��ͼ2����![]() , AB+BD��DE�Ƿ��ڣ�1���еĹ�ϵ�������ڣ������֤�����������ڣ���˵�����ɡ�
, AB+BD��DE�Ƿ��ڣ�1���еĹ�ϵ�������ڣ������֤�����������ڣ���˵�����ɡ�
(3) ��![]() ����AB+AE��AD+BE�������Ĺ�ϵ����AB+AE AD+BE ������>��,��<������=����
����AB+AE��AD+BE�������Ĺ�ϵ����AB+AE AD+BE ������>��,��<������=����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
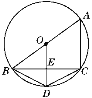
����Ŀ����ͼ���ı���ABDC�ǡ�O���ڽ��ı��Σ�AB�ǡ�O��ֱ����OD��BC��E.
(1)����д���ĸ���ͬ���͵���ȷ���ۣ�
(2)��BE��4��AC��6����DE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������OABC�Ķ���A��C�ֱ���x��y����������ϣ���DΪ�Խ���OB���е㣬��E��4��n���ڱ�AB�ϣ�����������![]() ��k��0���ڵ�һ�����ڵ�ͼ����D��E����tan��BOA=
��k��0���ڵ�һ�����ڵ�ͼ����D��E����tan��BOA=![]() ��
��
��1�����AB�ij���
��2�����������Ľ���ʽ��n��ֵ��
��3����������������ͼ������εı�BC���ڵ�F���������۵���ʹ��O���F�غϣ��ۺ۷ֱ���x��y�������ύ�ڵ�H��G�����߶�OG�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�������������У���B����3����1������Ҫ��ش��������⣺

��1����ͼ�н�����ȷ��ƽ��ֱ������ϵ��
��2������������������ϵ��д��A��C�����ꣻ
��3������ABC���ܳ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC������ACB��90����AC��BC����ABC�ĸ�CD���ƽ����AE�ཻ��F������C��CH��AE��G����AB��H��
��1������BCH�Ķ�����
��2����֤��CE��BH��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ϸ�Ĺ۲�ͼ�Σ����������ʽ��Ȼ�������⣺
OA1=1������
OA2=![]() ������ S1=
������ S1=![]() ��1��1=
��1��1=![]() ��
��
OA3=![]() ����������S2=
����������S2=![]() ��
��![]() ��1=
��1=![]() ��
��
OA4=![]() ����������S3=
����������S3=![]() ��
��![]() ��1=
��1=![]() ��
��
��1�������OA10=�� ����
��2����һ�������ε������![]() �������ǵ� ���������Σ�
�������ǵ� ���������Σ�
��3���ú�n��n�����������ĵ�ʽ��ʾ��������仯���ɣ�
��4�����S12+S22+S23+��+S2100��ֵ��

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com