
【题目】A市有近20年的马拉松比赛历史,过去全程马拉松名额一直相对较少。而近几年,这一现状大大改变,很多想参加全程马拉松(简称全马)的跑者报不上名。所以该城市近两年也大幅增加“全马”的名额。2017年,参加“全马”的人数比“半马”的人少,但是2018年,2019年参加“全马”的人数呈上升趋势,且每年比前一年均增加25%(即2018年比2017年增加25%,2019年比2018年增加25%),2019年,有12500名“全马”参赛者。
(1)求2017年、2018年“全马”参赛人数;
(2)据赞助食物的某商家反映:2017年与2018年该商家分别给参加“全马”和“半马”的参赛者提供了不同价格的食物,每个“全马”参赛者获得的食物价值高于“半马”参赛者,2017年,商家提供食物共用去22万元;这两年商家是按同一个标准分别给“全马”和“半马”参赛者提供食物(人太多,标准不可轻易提高),即使这样,2018年,虽然参加马拉松比赛的总人数与2017年一样多,但是由于“全马”参赛者人数刚好与“半马”参赛者人数调换了,赞助商比2017年多提供了p万元的食物;商家发现这p万元的食物刚好可以供400名“全马”参赛者和400名“半马”参赛者享用。求p的值。
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为1,AC,BD是对角线,将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.则下列结论:
①四边形AEGF是菱形;②△HED的面积是1﹣![]() ;③∠AFG=112.5°;④BC+FG=
;③∠AFG=112.5°;④BC+FG=![]() .其中正确的结论是( )
.其中正确的结论是( )
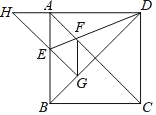
A. ①②③ B. ①②④ C. ①③④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数![]() 是关于
是关于![]() 的二次函数.求:
的二次函数.求:
![]() 满足条件的
满足条件的![]() 的值;
的值;
![]() 为何值时,抛物线有最低点?求出这个最低点,这时当
为何值时,抛物线有最低点?求出这个最低点,这时当![]() 为何值时,
为何值时,![]() 随
随![]() 的增大而增大?
的增大而增大?
![]() 为何值时,函数有最大值?最大值是多少?这时当
为何值时,函数有最大值?最大值是多少?这时当![]() 为何值时,
为何值时,![]() 随
随![]() 的增大而减小?
的增大而减小?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=2,∠B=∠C=40°,点D在线段BC上运动(D不与B、C重合),连接AD,作∠ADE=40°,DE交线段AC于E.
(1)当∠BDA=115°时,∠EDC= °,∠DEC= °;点D从B向C运动时,∠BDA逐渐变 (填“大”或“小”);
(2)当DC等于多少时,△ABD≌△DCE,请说明理由;
(3)在点D的运动过程中,△ADE的形状可以是等腰三角形吗?若可以,请直接写出∠BDA的度数.若不可以,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:平面直角坐标系中,点A(a,b)的坐标满足|a﹣b|+b2﹣8b+16=0.

(1)如图1,求证:OA是第一象限的角平分线;
(2)如图2,过A作OA的垂线,交x轴正半轴于点B,点M、N分别从O、A两点同时出发,在线段OA上以相同的速度相向运动(不包括点O和点A),过A作AE⊥BM交x轴于点E,连BM、NE,猜想∠ONE与∠NEA之间有何确定的数量关系,并证明你的猜想;
(3)如图3,F是y轴正半轴上一个动点,连接FA,过点A作AE⊥AF交x轴正半轴于点E,连接EF,过点F点作∠OFE的角平分线交OA于点H,过点H作HK⊥x轴于点K,求2HK+EF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,梯形ABCD中,AB∥CD,∠A=90°,E在AD上,且CE平分∠BCD,BE平分∠ABC,则下列关系式中成立的有( )
①![]() ; ②
; ②![]() ;③
;③![]() ;④
;④![]() ; ⑤
; ⑤![]()

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等边△ABC中,点D为射线BA上一点,作DE=DC,交直线BC于点E,∠ABC的平分线BF交CD于点F,过点A作AH⊥CD于H,当EDC=30![]() ,CF=
,CF=![]() ,则DH=______.
,则DH=______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com