
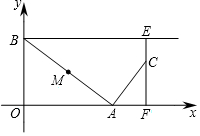
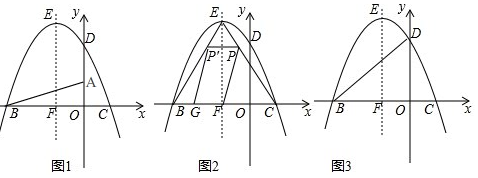
 如图,点A是x轴非负半轴上的动点,点B坐标为(0,4),M是线段AB的中点,将点M绕点A顺时针方向旋转90°得到点C,过点C作x轴的垂线,垂足为F,过点B作y轴的垂线与直线CF相交于点E,连接AC,BC,设点A的横坐标为t.
如图,点A是x轴非负半轴上的动点,点B坐标为(0,4),M是线段AB的中点,将点M绕点A顺时针方向旋转90°得到点C,过点C作x轴的垂线,垂足为F,过点B作y轴的垂线与直线CF相交于点E,连接AC,BC,设点A的横坐标为t.分析 (I)作辅助线,分别求OG和MG的长即可;
(II)如图1,同理可求得AG和OG的长,证明△AMG≌△CAF,得:AG=CF=$\frac{1}{2}$t,AF=MG=2,分别表示EC和BE的长,代入面积公式可求得S与t的关系式;并求其t的取值范围;
(III)证明△ABO∽△CAF,根据勾股定理表示AC和BC的长,计算其和,根据二次根式的意义得出当t=0时,值最小.
解答 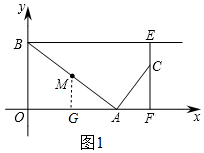 解:(I)如图1,过M作MG⊥OF于G,
解:(I)如图1,过M作MG⊥OF于G,
∴MG∥OB,
当t=2时,OA=2,
∵M是AB的中点,
∴G是AO的中点,
∴OG=$\frac{1}{2}$OA=1,MG是△AOB的中位线,
∴MG=$\frac{1}{2}$OB=$\frac{1}{2}$×4=2,
∴M(1,2);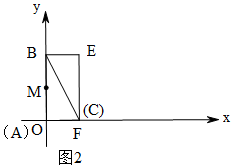
(II)如图1,同理得:OG=AG=$\frac{1}{2}$t,
∵∠BAC=90°,
∴∠BAO+∠CAF=90°,
∵∠CAF+∠ACF=90°,
∴∠BAO=∠ACF,
∵∠MGA=∠AFC=90°,MA=AC,
∴△AMG≌△CAF,
∴AG=CF=$\frac{1}{2}$t,AF=MG=2,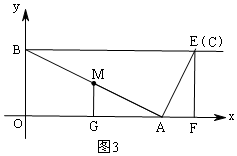
∴EC=4-$\frac{1}{2}$t,BE=OF=t+2,
∴S=S△BCE=$\frac{1}{2}$EC•BE=$\frac{1}{2}$(4-$\frac{1}{2}$t)(t+2)=-$\frac{1}{4}$t2+$\frac{3}{2}$t+4;
当A与O重合,C与F重合,如图2,此时t=0,
当C与E重合时,如图3,AG=EF,
即$\frac{1}{2}$t=4,
t=8,
∴S与t之间的函数关系式为:S=-$\frac{1}{4}$t2+$\frac{3}{2}$t+4(0≤t≤8);
(III)如图1,易得△ABO∽△CAF,
∴$\frac{AB}{AC}=\frac{OB}{AF}=\frac{OA}{FC}$=2,
∴AF=2,CF=$\frac{1}{2}$t,
由勾股定理得:AC=$\sqrt{A{F}^{2}+C{F}^{2}}$=$\sqrt{{2}^{2}+(\frac{1}{2}t)^{2}}$=$\sqrt{4+\frac{1}{4}{t}^{2}}$,
BC=$\sqrt{B{E}^{2}+E{C}^{2}}$=$\sqrt{(t+2)^{2}+(4-\frac{1}{2}t)^{2}}$=$\sqrt{5(\frac{1}{4}{t}^{2}+4)}$,
∴BC+AC=($\sqrt{5}$+1)$\sqrt{\frac{1}{4}{t}^{2}+4}$,
∴当t=0时,BC+AC有最小值.
点评 本题考查了坐标平面内几何图形的多种性质,难度适中.涉及到的知识点包括相似三角形、全等三角形、点的坐标、几何变换(旋转)、三角形的中位线等,第(3)问还考查了几何图形的空间想象能力.本题涉及考点众多,内涵丰富,对考生的数学综合能力要求较高.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
 二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(-1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a+c>3b;(3)8a+7b+2c>0;(4)若点A(-3,y1)、点B(-$\frac{1}{2}$,y2)、点C($\frac{7}{2}$,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x-5)=-3的两根为x1和x2,且x1<x2,则x1<-1<5<x2.其中正确的结论是①③⑤.
二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(-1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a+c>3b;(3)8a+7b+2c>0;(4)若点A(-3,y1)、点B(-$\frac{1}{2}$,y2)、点C($\frac{7}{2}$,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x-5)=-3的两根为x1和x2,且x1<x2,则x1<-1<5<x2.其中正确的结论是①③⑤.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
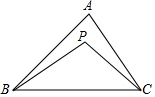 如图,BP与CP相交于点P,∠ABP=$\frac{1}{4}$∠ABC,∠ACP=$\frac{1}{4}$∠ACB,∠A=68°,那么∠P=96°.
如图,BP与CP相交于点P,∠ABP=$\frac{1}{4}$∠ABC,∠ACP=$\frac{1}{4}$∠ACB,∠A=68°,那么∠P=96°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com