
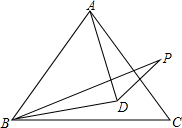
 如图所示,在等边△ABC中,BD平分∠PBC,且DB=DA,则∠BPD的度数是( )
如图所示,在等边△ABC中,BD平分∠PBC,且DB=DA,则∠BPD的度数是( )| A. | 20° | B. | 30° | C. | 40° | D. | 无法计算 |
分析 如图,连接DC、PC.先证明△ACD≌△BCD,则∠2=∠3,∠ADC=∠BDC;然后利用全等三角形的判定定理SSS证得△BDC≌△BDP,所以它们的对应角相等.
解答 解:如图,连接DC、PC.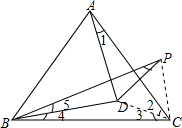
∵DA=DB,
∴∠DAB=∠DBA,
∵△ABC是等边三角形,
∴∠CAB=∠CBA=∠ACB=60°,AC=BC,
∴∠1=∠4.
∴在△ACD与△BCD中,$\left\{\begin{array}{l}{DA=DB}\\{∠1=∠4}\\{AC=BC}\end{array}\right.$,
∴△ACD≌△BCD(SAS),
∴∠2=∠3=30°,
∵BD平分∠PBC,
∴∠4=∠5,
∵BP=BC,
∴∠BPC=∠BCP,
∴∠DPC=∠DCP,
∴∠BPD=∠3.
∴∠BPD=30°,
故选B
点评 本题考查了全等三角形的判定与性质以及等腰三角形的性质.在应用全等三角形的判定时,要注意三角形间的公共边和公共角,必要时添加适当辅助线构造三角形.


科目:初中数学 来源: 题型:解答题
 如图,AB为⊙O的直径,弦CD⊥AB于点E,点G是$\widehat{AD}$上一点,连结AG,CG.
如图,AB为⊙O的直径,弦CD⊥AB于点E,点G是$\widehat{AD}$上一点,连结AG,CG.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{3}{1-a}$ | B. | $\frac{3}{a-1}$ | C. | $\frac{1}{1-a}$ | D. | $\frac{1}{a-1}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ax2+bx+c=0 | B. | $\frac{1}{{x}^{2}}$+$\frac{1}{x}$=2 | C. | x2+2x=x2-1 | D. | 3(x+1)2=2(x+1) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,△ABC内接于⊙O,AB是⊙O的直径,∠B=30°,CE平分∠ACB交⊙O于E,交AB于点D,连接AE,则AE:BC的值等于( )
如图,△ABC内接于⊙O,AB是⊙O的直径,∠B=30°,CE平分∠ACB交⊙O于E,交AB于点D,连接AE,则AE:BC的值等于( )| A. | 1:$\sqrt{2}$ | B. | $\sqrt{2}$:$\sqrt{3}$ | C. | $\sqrt{2}$:2 | D. | 2:3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,CD是Rt△ABC斜边上的高,∠ACB=90°,BC=2,AB=3.
如图,CD是Rt△ABC斜边上的高,∠ACB=90°,BC=2,AB=3.查看答案和解析>>
科目:初中数学 来源:2017届湖南津市中考数学模拟试卷(2)(解析版) 题型:解答题
雾霾天气严重影响市民的生活质量,因此,空气质量备受人们关注,甲城某空气质量监测站点检测了该区域每天的空气质量情况,统计了2015年2月—5月份若干天的情况,并制订了如下两幅不完整的统计图,请根据图中信息,解答下列问题:
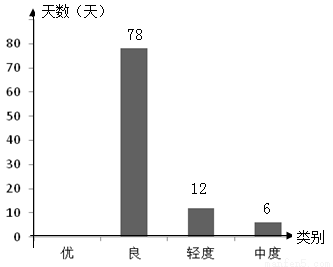

(1)统计图共统计了________天空气质量的情况.
(2)请将图中所缺部分补充完整,并计算空气质量为优的所在扇形的圆心角的度数?
(3)计算轻度污染的所占比例,并以此估计2016年2—5月份中大约有多少天受轻度污染?(最后结果用收尾法)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com