Question

10．如图（1），在Rt△AOB中，∠A=90°，∠AOB=60°，OB=2$\sqrt{3}$，∠AOB的平分线OC交AB于C，过O点做与OB垂直的直线ON．动点P从点B出发沿折线BC-CO向终点O运动，运动时间为t秒，同时动点Q从点C出发沿线段CO及直线ON运动，当点P到达点O时P、Q同时停止运动．
（1）求OC、BC的长；
（2）当点P与点Q的速度都是每秒1个单位长度的速度运动时，设△CPQ的面积为S，求S与t的函数关系式；
（3）当点P运动到OC上时，在直线OB上有一点D，当PD+BP最小时，在直线OB上有一点E，若以B、P、Q、E为顶点的四边形为平行四边形，设点P、Q的运动路程分别为a、b，求a与b满足的数量关系．

Answer 1

分析 （1）求出∠B，根据直角三角形性质求出OA，求出AB，在△AOC中，根据勾股定理得出关于OC的方程，求出OC即可；
（2）有四种情况：①当P在BC上，Q在OC上时，t＜2，过P作PH⊥OC于H，求出PH，根据三角形的面积公式求出即可；②当t=2时，P在C点，Q在O点，此时，△CPQ不存在；③当P在OC上，Q在ON上时，过P作PG⊥ON于G，过C作CZ⊥ON于Z，求出CZ和PG的值，求出△OCQ和△OPQ的面积，相减即可④t=4时，求出即可；
（3）过B作BB₁⊥OC，垂足为C₁，与OA的延长线交于B₁，作B₁D⊥OB，垂足为D，与OC交于点P，此时BP+PD=B₁D（最短），于是得到△OBB₁为正三角形，①当点Q在OC上时，由PQ与EB交于点O⇒BPQE不可能为平行四边形，②当点Q在直线ON上时，A．如图（4）以BQ为对角线，B．如下图（5）以BP为对角线，C．如下图（6）以BE为对角线，根据平行四边形的性质得到a+b=5．

解答 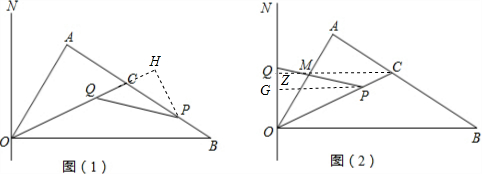（1）解：∵∠A=90°，∠AOB=60°，OB=2$\sqrt{3}$，
∴∠B=30°，
∴OA=$\frac{1}{2}$OB=$\sqrt{3}$，
由勾股定理得：AB=3，
∵OC平分∠AOB，
∴∠AOC=∠BOC=30°=∠B，
∴OC=BC，
在△AOC中，AO²+AC²=CO²，
∴（$\sqrt{3}$）²+（3-OC）²=OC²，
∴OC=2=BC，
答：OC=2，BC=2．

（2）解：①如图（1），当P在BC上，Q在OC上时，0＜t＜2，
则CP=2-t，CQ=t，
过P作PH⊥OC于H，
∠HCP=60°，
∠HPC=30°，
∴CH=$\frac{1}{2}$CP=$\frac{1}{2}$（2-t），HP=$\frac{\sqrt{3}}{2}$（2-t），
∴S_△CPQ=$\frac{1}{2}$CQ×PH=$\frac{1}{2}$×t×$\frac{\sqrt{3}}{2}$（2-t），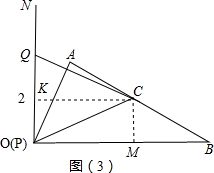
即S=-$\frac{\sqrt{3}}{4}$t²+$\frac{\sqrt{3}}{2}$t；
②当t=2时，P在C点，Q在O点，此时，△CPQ不存在，
∴S=0，

③如图（2）当P在OC上，Q在ON上时2＜t＜4，
过P作PG⊥ON于G，过C作CZ⊥ON于Z，
∵CO=2，∠NOC=60°，
∴CZ=$\sqrt{3}$，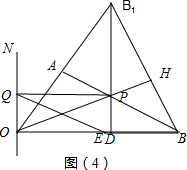
CP=t-2，OQ=t-2，
∠NOC=60°，
∴∠GPO=30°，
∴OG=$\frac{1}{2}$OP=$\frac{1}{2}$（4-t），PG=$\frac{\sqrt{3}}{2}$（4-t），
∴S_△CPQ=S_△COQ-S_△OPQ=$\frac{1}{2}$×（t-2）×$\sqrt{3}$-$\frac{1}{2}$×（t-2）×$\frac{\sqrt{3}}{2}$（4-t），
即S=$\frac{\sqrt{3}}{4}$t²-$\sqrt{3}$t+$\sqrt{3}$．
④当t=4时，P在O点，Q在ON上，如图（3）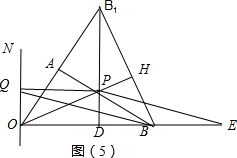

过C作CM⊥OB于M，CK⊥ON于K，
∵∠B=30°，由（1）知BC=2，
∴CM=$\frac{1}{2}$BC=1，
有勾股定理得：BM=$\sqrt{3}$，
∵OB=2$\sqrt{3}$，
∴OM=2$\sqrt{3}$-$\sqrt{3}$=$\sqrt{3}$=CK，
∴S=$\frac{1}{2}$PQ×CK=$\frac{1}{2}$×2×$\sqrt{3}$=$\sqrt{3}$；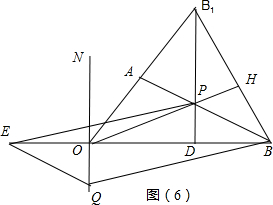
综合上述：S与t的函数关系式是：${S_{△CPQ}}=\left\{\begin{array}{l}-\frac{{\sqrt{3}}}{4}{t^2}+\frac{{\sqrt{3}}}{2}t\;\;\;\;\;\;\;\;\;\;\;\;\;（0≤t≤2）\\-\frac{{\sqrt{3}}}{4}{t^2}+\frac{{3\sqrt{3}}}{2}t-2\sqrt{3}\;\;（t＞2）\end{array}\right.$；
（3）过B作BB₁⊥OC，垂足为C₁，与OA的延长线交于B₁，
作B₁D⊥OB，垂足为D，与OC交于点P，此时BP+PD=B₁D（最短），
由题可得：△OBB₁为正三角形，
当P与C重合，D为OB中点，PD=CA=1，BP+PD=3，
①当点Q在OC上时，由PQ与EB交于点O⇒BPQE不可能为平行四边形，
②当点Q在直线ON上时，
A．如图（4）以BQ为对角线，∵QE∥PB．QE=PB，E与D重合，∴OQ=PD=1，
此时a+b=5，
B．如下图（5）以BP为对角线，∵QP∥BE，QP=BE，∴PQ=BE=$\sqrt{3}$，
此时a+b=5，
C．如下图（6）以BE为对角线，∵PB∥EQ，PB=EQ，解Rt△EOQ得OQ=1，
此时a+b=5，
综上：以B、P、Q、E为顶点的四边形为平行四边形时Q在直线ON上且a+b=5．

点评 本题考查了等腰三角形的性质，三角形的面积，函数自变量的取值范围，解一元一次方程，勾股定理，含30度角的直角三角形性质等知识点的运用，本题综合性比较强，难度偏大，主要考查了学生综合运用性质进行推理和计算的能力，并且运用了方程思想和分类讨论思想．