
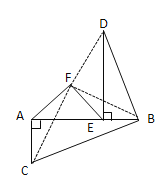
【题目】已知:AB⊥AC,DE⊥AB,AC=BE,BC=BD,

(1)求证:BC⊥BD;
(2)若点F是BC,BD的垂直平分线的交点,连接FA、FE.填空:判断△AFE的形状是_____.
【答案】(1)证明见解析;(2)等腰直角三角形
【解析】
(1)利用HL定理证明Rt△ABC≌Rt△EDB,然后得到∠D=∠ABC,从而求证;(2)连接FC,FB,FD,利用垂直平分线的性质
证明:(1)∵AB⊥AC,DE⊥AB
∴∠CAB=∠BED=90°
在Rt△ABC≌Rt△EDB中,![]()
∴Rt△ABC≌Rt△EDB(HL)
∴∠D=∠ABC
又∵∠DBE+∠ABC=90°
∴∠D+∠ABC=90°
∴∠CBD=90°
即BC⊥BD;
(2)连接FC,FB,FD,
∵点F是BC,BD的垂直平分线的交点
∴FC=FB=FD
∴∠CBF=∠FCB
又∵BC=BD,BF=BF
∴△BCF≌△BDF
又∵∠CBD=90°
∴∠DBF=∠CBF=45°
∴∠FCB=∠DBF=∠CBF=45°
∴∠CFB=90°
又∵Rt△ABC≌Rt△EDB
∴∠ACB=∠DBE,AC=BE
∴∠ACF=∠EBF
又∵FC=FB
∴△FAC≌△FEB
∴FA=FE,∠AFC=∠EFB
∵∠CFB=90°
∴∠CFE+∠EFB=90°
∴∠AFC+∠EFB=90°
即∠AFE=90°
即△AFE是等腰直角三角形


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD中,已知AD =8,折叠纸片使AB边与对角线AC
重合,点B落在点F处,折痕为AE,且EF=3,则AB的长为( )

A. 3 B. 4
C. 5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
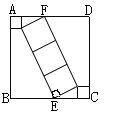
【题目】如图,在边长为7的正方形ABCD中放入五个小正方形后形成一个中心对称图形,其中两顶点E、F分别在边BC、AD上,则放入的五个小正方形的面积之和为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
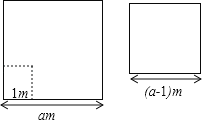
【题目】如图,“主收1号”小麦的试验田是边长为am(a>1)的正方形去掉一个边长为1m的正方形蓄水池后余下的部分,“丰收2号”小麦的试验田是边长为(a﹣1)m的正方形,两块试验田的小麦都收获了500kg.
(1)哪种小麦的单位面积产量高?
(2)若高的单位面积产量是低的单位面积产量的![]() (kg)倍,求a的值
(kg)倍,求a的值
(3)利用(2)中所求的a的值,分解因式x2﹣ax﹣108=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果批发商销售每箱进价为40元的苹果,物价部门规定每箱售价不得高于55元,市场调查发现,若每箱以50元的价格调查,平均每天销售90箱,价格每提高1元,平均每天少销售3箱.
(1)求平均每天销售量y(箱)与销售价x(元/箱)之间的函数关系式.
(2)求该批发商平均每天的销售利润w(元)与销售价x(元/箱)之间的函数关系式.
(3)当每箱苹果的销售价为多少元时,可以获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为美化校园,计划对面积为1800m2的区域进行绿化,安排甲、乙两个工程队完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍,并且在独立完成面积为400 m2区域的绿化时,甲队比乙队少用4天.
(1)求甲、乙两工程队每天能完成绿化的面积分别是多少m2?
(2)若学校每天需付给甲队的绿化费用是0.4万元,乙队为0.25万元,要使这次的绿化总费用不超过8万元,至少应安排甲队工作多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
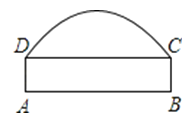
【题目】如图,有一条双向公路隧道,其横断面由抛物线和矩形ABCD的三边DA、AB、BC围成,隧道最大高度为4.9米,AB=10米,BC=2.4米,若有一辆高为4米、宽为2米的集装箱的汽车要通过隧道,为了使箱顶不碰到隧道顶部,又不违反交通规则(汽车应靠道路右侧行驶,不能超过道路中线),汽车的右侧必须离开隧道右壁几米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,矩形OABC的顶点A、B在双曲线y=![]() ( x>0)上,BC与x轴交于点D.若点A的坐标为(1,2),则点B的坐标为( )
( x>0)上,BC与x轴交于点D.若点A的坐标为(1,2),则点B的坐标为( )
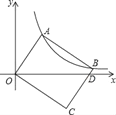
A. (3,![]() ) B. (4,
) B. (4,![]() ) C. (
) C. (![]() ,
,![]() ) D. (5,
) D. (5,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com