
【题目】如图,抛物线的顶点坐标为C(0,8),并且经过A(8,0),点P是抛物线上点A,C间的一个动点(含端点),过点P作直线y=8的垂线,垂足为点F,点D,E的坐标分别为(0,6),(4,0),连接PD,PE,DE.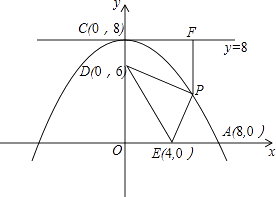
(1)求抛物线的解析式;
(2)猜想并探究:对于任意一点P,PD与PF的差是否为固定值?如果是,请求出此定值;如果不是,请说明理由;
(3)求:①当△PDE的周长最小时的点P坐标;②使△PDE的面积为整数的点P的个数.
【答案】
(1)解:设抛物线的解析式为y=ax2+8.
∵经过点A(8,0),
∴64a+8=0,解得a=﹣ ![]() .
.
抛物线的解析式为:y=﹣ ![]() x2+8
x2+8
(2)解:PD与PF的差是定值.
理由如下:设P(a,﹣ ![]() a2+8),则F(a,8),
a2+8),则F(a,8),
∵D(0,6),
∴PD= ![]() =
= ![]() =
= ![]() a2+2,PF=8﹣(
a2+2,PF=8﹣( ![]() )=
)= ![]() .
.
∴PD﹣PF=2.
(3)解:①当点P运动时,DE大小不变,则PE与PD的和最小时,△PDE的周长最小,
∵PD﹣PF=2,
∴PD=PF+2,
∴PE+PD=PE+PF+2,
∴当P、E、F三点共线时,PE+PF最小,此时点P,E的横坐标都为4,
∵将x=4代入y=﹣ ![]() x2+8,得y=6,
x2+8,得y=6,
∴P(4,6),此时△PDE的周长最小.
②如图1所示:过点P做PH⊥x轴,垂足为H.
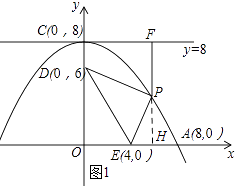
设P(a,﹣ ![]() a2+8)
a2+8)
∴PH=﹣ ![]() a2+8,EH=a﹣4,OH=a
a2+8,EH=a﹣4,OH=a
S△DPE=S梯形PHOD﹣S△PHE﹣S△DOE= ![]() a(﹣
a(﹣ ![]() a2+8+6)﹣
a2+8+6)﹣ ![]() (
( ![]() +8)(a﹣4)﹣
+8)(a﹣4)﹣ ![]() ×4×6=﹣
×4×6=﹣ ![]() a2+3a+4=﹣
a2+3a+4=﹣ ![]() (a﹣6)2+13.
(a﹣6)2+13.
∵点P是抛物线上点A,C间的一个动点(含端点),
∴0≤a≤8,
∴当a=6时,S△DPE取最大值为13.当a=0时,S△DPE取最小值为4.即4≤S△DPE≤13,其中,当S△DPE=12时,有两个点P.
∴共有11个令S△DPE为整数的点.
【解析】(1)此抛物线的顶点在y轴上,因此设此抛物线解析式为y=ax2+k,将点A、点B的坐标分别代入,就可求出函数解析式。
(2)抓住PF⊥直线y=8,设出点P、点F的坐标,用含a的代数式分别表示出PD、PF的长,再求出它们的差即可。
(3)①要使△PDE的周长最小,而DE的长是一个定值,关键是DP+PE的值要最小,由(2)可知PD=PF+2,即PE+PD=PE+PF+2,根据两点之间线段最短,P、E、F三点共线时,PE+PF最小,此时点P,E的横坐标都为4,代入函数解析式即可求出点P的坐标。②过点P做PH⊥x轴,垂足为H,设出点P的坐标,分别表示出PH、EH、的长,再求出S△DPE与a的函数关系式,根据点P是抛物线上点A,C间的一个动点(含端点),求出a的取值范围,继而求出S△DPE的取值范围,即可求出结果。
【考点精析】本题主要考查了二次函数的最值和勾股定理的概念的相关知识点,需要掌握如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能正确解答此题.


 新思维寒假作业系列答案
新思维寒假作业系列答案科目:初中数学 来源: 题型:
【题目】为发展电信事业,方便用户,电信公司对移动电话采取不同的收费方式,其中,所使用的“便民卡”与“如意卡”在某市范围内每月(30天)的通话时间x(min)与通话费y(元)的关系如图所示:
(1)分别求出通话费y1 , y2与通话时间x之间的函数关系式;
(2)请帮用户计算,在一个月内使用哪一种卡便宜.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,O是坐标原点,ABCD的顶点A的坐标为(﹣2,0),点D的坐标为(0,2 ![]() ),点B在x轴的正半轴上,点E为线段AD的中点
),点B在x轴的正半轴上,点E为线段AD的中点
(1)如图1,求∠DAO的大小及线段DE的长;
(2)过点E的直线l与x轴交于点F,与射线DC交于点G.连接OE,△OEF′是△OEF关于直线OE对称的图形,记直线EF′与射线DC的交点为H,△EHC的面积为3 ![]() .
.
①如图2,当点G在点H的左侧时,求GH,DG的长;
②当点G在点H的右侧时,求点F的坐标(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P为定角∠AOB的平分线上的一个定点,且∠MPN与∠AOB互补,若∠MPN在绕点P旋转的过程中,其两边分别与OA、OB相交于M、N两点,则以下结论:(1)PM=PN恒成立;(2)OM+ON的值不变;(3)四边形PMON的面积不变;(4)MN的长不变,其中正确的个数为( )

A. 4B. 3C. 2D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人共同计算一道整式乘法题:(2x+a)(3x+b).甲由于把第一个多项式中的“+a”看成了“﹣a”,得到的结果为6x2+11x﹣10;乙由于漏抄了第二个多项式中x的系数,得到的结果为2x2﹣9x+10.
(1)求a、b的值.
(2)计算这道乘法题的正确结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在长方形ABCD中, AB=CD=4cm,BC=3cm,动点P从点A出发,先以1cm/s的速度沿A→B,然后以2cm/s的速度沿B→C运动,到C点停止运动,设点P运动的时间为t秒,是否存在这样的t,使得△BPD的面积S>3cm2?如果能,请求出t的取值范围;如果不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】描点画图是探究未知函数图象变化规律的一个重要方法,下面是通过描点画图感知函数![]() 图象的变化规律的过程:
图象的变化规律的过程:
|
|
|
|
|
|
|
| … |
|
|
|
|
|
|
|
| … |
(1)如表是________与________的几组对应值,则:m=________;
(2)根据表中的数据,在平面直角坐标系![]() 中描出还未描出的点,并画出该函数的图象:
中描出还未描出的点,并画出该函数的图象:

(3)从函数图象可以看出,当________![]() 时,________随着________的增大而________(填增大或减小).
时,________随着________的增大而________(填增大或减小).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com