
分析 ①分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
②先计算乘方和乘法,再计算加减可得.
解答 解:①解不等式组:$\left\{\begin{array}{l}{2-x>0}&{①}\\{\frac{5x+1}{2}+1≥\frac{2x-1}{3}}&{②}\end{array}\right.$,
解不等式①,得x<2.
解不等式②,得x≥-1,
所以,不等式组的解集是-1≤x<2.
②:原式=-1+2-$\sqrt{3}$+2-5=-2-$\sqrt{3}$.
点评 本题考查的是解一元一次不等式组和实数的混合运算,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
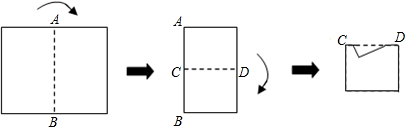
| A. | 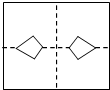 | B. | 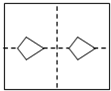 | C. | 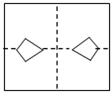 | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
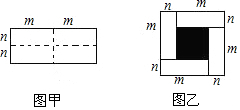 已知图甲是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均匀分成四小块长方形,然后按图乙的形状拼成一个正方形.
已知图甲是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均匀分成四小块长方形,然后按图乙的形状拼成一个正方形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com