
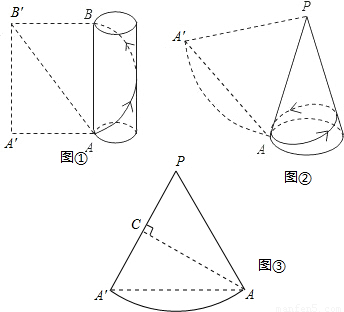
 ,高为4的圆柱体和它的侧面展开图,AB是圆柱的一条母线,一只蚂蚁从A点出发沿圆柱的侧面爬行一周到达B点,求蚂蚁爬行的最短路程.(探究思路:将圆柱的侧面沿母线AB剪开,它的侧面展开图如图①中的矩形ABB′A′,则蚂蚁爬行的最短路程即为线段AB′的长);
,高为4的圆柱体和它的侧面展开图,AB是圆柱的一条母线,一只蚂蚁从A点出发沿圆柱的侧面爬行一周到达B点,求蚂蚁爬行的最短路程.(探究思路:将圆柱的侧面沿母线AB剪开,它的侧面展开图如图①中的矩形ABB′A′,则蚂蚁爬行的最短路程即为线段AB′的长); ,母线长为4的圆锥和它的侧面展开图,PA是它的一条母线,一只蚂蚁从A点出发沿圆锥的侧面爬行一周后回到A点,求蚂蚁爬行的最短路程;
,母线长为4的圆锥和它的侧面展开图,PA是它的一条母线,一只蚂蚁从A点出发沿圆锥的侧面爬行一周后回到A点,求蚂蚁爬行的最短路程;
 解:(1)∵BB′=2π×
解:(1)∵BB′=2π×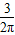 =3,
=3,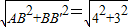 =5.
=5.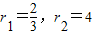 ,
, ,即
,即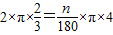 ,
,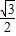 =
=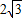 ,
,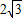 .
.

 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源:2011年3月湖北省鄂州市鄂城区燕矶中学九年级(下)月考数学试卷(解析版) 题型:解答题
| A | B | |
| 价格(万元/台) | 6 | 5 |
| 日产量(万件/台) | 6 | 4 |
查看答案和解析>>
科目:初中数学 来源:2009年全国中考数学试题汇编《不等式与不等式组》(05)(解析版) 题型:解答题
| A | B | |
| 价格(万元/台) | 6 | 5 |
| 日产量(万件/台) | 6 | 4 |
查看答案和解析>>
科目:初中数学 来源:2009年湖南省永州市中考数学试卷(解析版) 题型:解答题
| A | B | |
| 价格(万元/台) | 6 | 5 |
| 日产量(万件/台) | 6 | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com