
分析 原式变形后,约分即可得到结果.
解答 解:原式=$\frac{(x-2)(x+1)+(x-1)\sqrt{x-2}•\sqrt{x+2}}{(x+2)(x-1)+(x+1)\sqrt{x-2}•\sqrt{x+2}}$
=$\frac{\sqrt{x-2}[\sqrt{x-2}(x+1)+(x-1)\sqrt{x+2}]}{\sqrt{x+2}[\sqrt{x+2}(x-1)+(x+1)\sqrt{x-2}]}$
=$\frac{\sqrt{x-2}}{\sqrt{x+2}}$=$\frac{\sqrt{{x}^{2}-4}}{x+2}$.
点评 此题考查了二次根式的化简求值,熟练掌握运算法则是解本题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
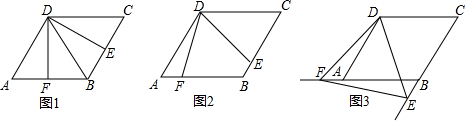
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
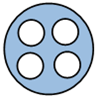 如图,在一块半径为R的圆形板材上,冲去半径为r的四个小圆,小刚测得R=6.8cm,r=1.6
如图,在一块半径为R的圆形板材上,冲去半径为r的四个小圆,小刚测得R=6.8cm,r=1.6查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com