

分析 (1)①先证明△ABC,△ACD都是等边三角形,再证明∠BCE=∠ACF即可解决问题.②根据①的结论得到BE=AF,由此即可证明.
(2)设DH=x,由题意,CD=2x,CH=$\sqrt{3}$x,由△ACE∽△HCF,得$\frac{AE}{FH}=\frac{AC}{CH}$由此即可证明.
(3)如图3中,作CN⊥AD于N,CM⊥BA于M,CM与AD交于点H.先证明△CFN∽△CEM,得出$\frac{CN}{CM}=\frac{FN}{EM}$,由AB•CM=AD•CN,AD:AD=1:4,推出CM=4CN,得出$\frac{CN}{CM}=\frac{FN}{EM}$=$\frac{1}{4}$,设CN=a,FN=b,则CM=4a,EM=4b,再求出AC,AE+4AF,即可解决问题.
解答 解;(1)AE+AF=AC,理由如下:
∵四边形ABCD是平行四边形,∠BAD=120°,
∴∠D=∠B=60°,
∵四边形ABCD是菱形,
∴AD=AB,
∴△ABC,△ACD都是等边三角形,
∴∠B=∠CAD=60°,∠ACB=60°,BC=AC,
∵∠ECF=60°,
∴∠BCE+∠ACE=∠ACF+∠ACE=60°,
∴∠BCE=∠ACF,
在△BCE和△ACF中,$\left\{\begin{array}{l}{∠B=∠CAF}&{\;}\\{BC=AC}&{\;}\\{∠BCE=∠ACF}&{\;}\end{array}\right.$,
∴△BCE≌△ACF(ASA).
∴BE=AF,
∴AE+AF=AE+BE=AB=AC;
故答案为:AE+AF=AC.
(2)设DH=x,由题意,CD=2x,CH=$\sqrt{3}$x,
∴AD=2AB=4x,
∴AH=AD-DH=3x,
∵CH⊥AD,
∴AC=$\sqrt{A{H}^{2}+C{H}^{2}}$=2$\sqrt{3}$x,
∴AC2+CD2=AD2,
∴∠ACD=90°,
∴∠BAC=∠ACD=90°,
∴∠CAD=30°,
∴∠ACH=60°,
∵∠ECF=60°,
∴∠HCF=∠ACE,
∴△ACE∽△HCF,
∴AE:FH=AC:CH=2:1.
(3)如图3中,作CN⊥AD于N,CM⊥BA于M,CM与AD交于点H.
∵∠ECF+∠EAF=180°,
∴∠AEC+∠AFC=180°,
∵∠AFC+∠CFN=180°,
∴∠CFN=∠AEC,∵∠M=∠CNF=90°,
∴△CFN∽△CEM,
∴$\frac{CN}{CM}=\frac{FN}{EM}$,
∵AB•CM=AD•CN,AB:AD=1:4,
∴CM=4CN,
∴$\frac{CN}{CM}=\frac{FN}{EM}$=$\frac{1}{4}$,
设CN=a,FN=b,则CM=4a,EM=4b,
∵∠MAH=60°,∠M=90°,
∴∠AHM=∠CHN=30°,
∴HC=2a,HM=2a,HN=$\sqrt{3}$a,
∴AM=$\frac{\sqrt{3}}{3}$HM=$\frac{2\sqrt{3}}{3}$a,AH=2AM=$\frac{4\sqrt{3}}{3}$a,
∴AC=$\sqrt{A{M}^{2}+C{M}^{2}}$=$\frac{2\sqrt{39}}{3}$a,
AE+4AF=(EM-AM)+4(AH+HN-FN)=EM-AM+4AH+4HN-4FN=4AH+4HN-AM=$\frac{26\sqrt{3}}{3}$a,
∴$\frac{AE+4AF}{AC}$=$\frac{\frac{26\sqrt{3}}{3}a}{\frac{2\sqrt{39}}{3}a}$=$\sqrt{13}$;
故答案为:$\sqrt{13}$.
点评 本题考查几何变换综合题.全等三角形的判定和性质.相似三角形的判定和性质、等边三角形的性质等知识,解题的关键是正确寻找全等三角形或相似三角形,学会添加常用辅助线,学会利用参数解决问题,属于中考压轴题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
 某校决定在4月7日开展“世界无烟日”宣传活动,活动有A社区板报、B集会演讲、C喇叭广播、D发宣传画四种宣传方式.学校围绕“你最喜欢的宣传方式是什么?”在全校学生中进行随机抽样调查(四个选项中必选且只选一项),根据调查统计结果,绘制了两种不完整的统计图表:
某校决定在4月7日开展“世界无烟日”宣传活动,活动有A社区板报、B集会演讲、C喇叭广播、D发宣传画四种宣传方式.学校围绕“你最喜欢的宣传方式是什么?”在全校学生中进行随机抽样调查(四个选项中必选且只选一项),根据调查统计结果,绘制了两种不完整的统计图表:| 选项 | 方式 | 百分比 |
| A | 社区板报 | 35% |
| B | 集会演讲 | m |
| C | 喇叭广播 | 25% |
| D | 发宣传画 | 10% |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 对角线互相垂直且相等的平行四边形是正方形 | |
| B. | 对角线互相垂直平分的四边形是菱形 | |
| C. | 对角线相等的四边形是矩形 | |
| D. | 对角线互相平分的四边形是平行四边形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 图(1)为一波浪式相框(厚度忽略不计),内部可插入占满整个相框的照片一张,如图(2),主视图(不含图中虚线部分)为两端首尾相连的等弧构成,左视图和俯视图均为长方形(单位:cm):
图(1)为一波浪式相框(厚度忽略不计),内部可插入占满整个相框的照片一张,如图(2),主视图(不含图中虚线部分)为两端首尾相连的等弧构成,左视图和俯视图均为长方形(单位:cm):查看答案和解析>>
科目:初中数学 来源: 题型:解答题
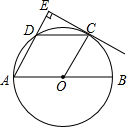 如图,AB是⊙O的直径,点C、D为半圆O的三等分点,过点C作CE⊥AD,交AD的延长线于点E.
如图,AB是⊙O的直径,点C、D为半圆O的三等分点,过点C作CE⊥AD,交AD的延长线于点E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,AB是⊙O的直径,点F、C是⊙O上两点,且$\widehat{AF}$=$\widehat{FC}$=$\widehat{CB}$,连接AC、AF,过点C作CD⊥AF,交AF的延长线于点D,垂足为D,若CD=2$\sqrt{3}$,则⊙O的半径为( )
如图,AB是⊙O的直径,点F、C是⊙O上两点,且$\widehat{AF}$=$\widehat{FC}$=$\widehat{CB}$,连接AC、AF,过点C作CD⊥AF,交AF的延长线于点D,垂足为D,若CD=2$\sqrt{3}$,则⊙O的半径为( )| A. | 2$\sqrt{3}$ | B. | 4$\sqrt{3}$ | C. | 2 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com