Question

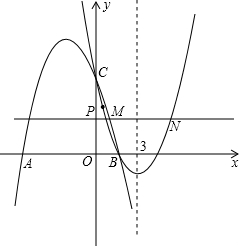
如图，已知抛物线y₁＝－2x²＋2，直线y₂＝2x＋2，当x任取一值时，x对应的函数值分别为y₁、y₂．若y₁≠y₂，取y₁、y₂中的较小值记为M；若y₁＝y₂，记M＝y₁＝y₂．例如：当x＝1时，y₁＝0，y₂＝4，y₁＜y₂，此时M＝0．下列判断：①当x＞0时，y₁＞y₂；②当x＜0时，x值越大，M值越小；③使得M大于2的x值不存在；④使得M＝1的x值是－或．

其中正确的是

[　　]

A．①②

B．①④

C．②③

D．③④

Answer 1

答案：D
解析：

解：∵①当x＞0时，利用函数图象可以得出y2＞y1；∴此选项错误； 　　∵抛物线y1＝－2x2＋2，直线y2＝2x＋2，当x任取一值时，x对应的函数值分别为y1、y2．若y1≠y2，取y1、y2中的较小值记为M； 　　∴②当x＜0时，根据函数图象可以得出x值越大，M值越大；∴此选项错误； 　　∵抛物线y1＝－2x2＋2，直线y2＝2x＋2，与y轴交点坐标为：(0，2)，当x＝0时，M＝2，抛物线y1＝－2x2＋2，最大值为2，故M大于2的x值不存在； 　　∴③使得M大于2的x值不存在，此选项正确； 　　∵使得M＝1时，可能是y1＝－2x2＋2＝1，解得：x1＝，x2＝－， 　　当y2＝2x＋2＝1，解得：x＝－， 　　由图象可得出：当x＝＞0，此时对应y2＝M， 　　∵抛物线y1＝－2x2＋2与x轴交点坐标为：(1，0)，(－1，0)， 　　∴当－1＜x＜0，此时对应y1＝M， 　　故M＝1时，x1＝，x＝－， 　　故④使得M＝1的x值是或．此选项正确； 　　故正确的有：③④．

提示：

二次函数综合题．