
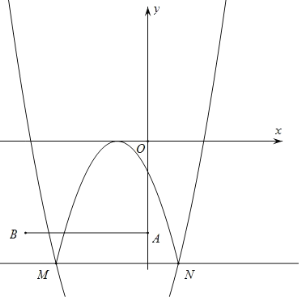
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕxOyжаЃЌХзЮяЯпy=x2+2x+aЉ3ЃЌЕБa=0ЪБЃЌХзЮяЯпгыyжсНЛгкЕуAЃЌНЋЕуAЯђзѓЦНвЦ4ИіЕЅЮЛГЄЖШЃЌЕУЕНЕуBЃЎ
ЃЈ1ЃЉЧѓЕуBЕФзјБъЃЛ
ЃЈ2ЃЉХзЮяЯпгыжБЯпy=aНЛгкMЁЂNСНЕуЃЌНЋХзЮяЯпдкжБЯпy=aЯТЗНЕФВПЗжбижБЯпy=aЗелЃЌЭМЯѓЕФЦфЫћВПЗжБЃГжВЛБфЃЌЕУЕНвЛИіаТЕФЭМЯѓЃЌМДЮЊЭМаЮMЃЎ
ЂйЧѓЯпЖЮMNЕФГЄЃЛ
ЂкШєЭМаЮMгыЯпЖЮABЧЁгаСНИіЙЋЙВЕуЃЌНсКЯКЏЪ§ЭМЯѓЃЌжБНгаДГіaЕФШЁжЕЗЖЮЇЃЎ
ЁОД№АИЁПЃЈ1ЃЉB(Љ4ЃЌЉ3)ЃЛЃЈ2ЃЉЂйMN=4ЃЛЂкЉ6ЃМaЃМЉ3Лђa=Љ7ЃЎ
ЁОНтЮіЁП
(1)ЧѓГіA(0ЃЌ-3)ЃЌМДПЩЕУЕНB(-4ЃЌ-3)ЃЛ
(2)Сю![]() МДПЩЧѓГіMNЕФГЄЃЛ
МДПЩЧѓГіMNЕФГЄЃЛ
(3)ЖЅЕу(![]() )ЃЌЙигк
)ЃЌЙигк![]() ЕФЖдГЦЕуЮЊ(
ЕФЖдГЦЕуЮЊ(![]() )ЃЌЕБ
)ЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌДЫЪБЭМаЮMгыЯпЖЮABЧЁгаСНИіЙЋЙВЕуЃЌЕБ
ЃЌДЫЪБЭМаЮMгыЯпЖЮABЧЁгаСНИіЙЋЙВЕуЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() Йигк
Йигк![]() ЗелВПЗжЕФКЏЪ§НтЮіЪНЮЊ
ЗелВПЗжЕФКЏЪ§НтЮіЪНЮЊ![]() ЃЌЕБ
ЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌЕБ
ЃЌЕБ![]() ЪБЃЌЭМаЮгы
ЪБЃЌЭМаЮгы![]() гаШ§ИіНЛЕуЃЌгЩДЫПЩжЊдк
гаШ§ИіНЛЕуЃЌгЩДЫПЩжЊдк![]() ЪБЃЌЭМаЮгы
ЪБЃЌЭМаЮгы![]() гаШ§ИіНЛЕуЃЌ
гаШ§ИіНЛЕуЃЌ![]() вЊдкЯпЖЮABЕФЯТЗНЃЌ
вЊдкЯпЖЮABЕФЯТЗНЃЌ![]() ЃЌЙЪ
ЃЌЙЪ![]() Чв
Чв![]() ЃЎ
ЃЎ
(1)ЕБa=0ЪБЃЌA(0ЃЌЉ3)ЃЌ
НЋЕуAЯђзѓЦНвЦ4ИіЕЅЮЛГЄЖШЃЌЕУЕНЕуBЃЌ
ЁрB(Љ4ЃЌЉ3)ЃЛ
(2)ЂйЁпХзЮяЯпy=x2+2x+aЉ3гыжБЯпy=aНЛгкMЁЂNСНЕуЃЌ
Ёрx2+2x+aЉ3=aМДx2+2xЉ3=0ЃЌ
НтЕУЃК![]() ЃЌ
ЃЌ
ЁрMN![]() ЃЛ
ЃЛ
ЂкЖЅЕу(Љ1ЃЌaЉ4)ЃЌЙигкy=aЕФЖдГЦЕуЮЊ(Љ1ЃЌa+4)ЃЌ
ЕБa+4=Љ3ЪБЃЌa=Љ7ЃЌ
ДЫЪБЭМаЮMгыЯпЖЮABЧЁгаСНИіЙЋЙВЕуЃЌ
ЯпЖЮABЕФСНИіЖЫЕуЮЊA(0ЃЌЉ3)ЃЌB(Љ4ЃЌЉ3)ЃЌ
ЕБa=Љ6ЪБЃЌy=x2+2xЉ9ЃЌy=Љ6ЃЌ
y=x2+2xЉ9Йигкy=Љ6ЗелВПЗжЕФКЏЪ§НтЮіЪНЮЊy=Љx2Љ2xЉ4ЃЌ
ЕБx=0ЪБЃЌy=Љ4ЃЌ
ЕБa=Љ6ЪБЃЌЭМаЮгыy=Љ6гаШ§ИіНЛЕуЃЌ
ЁрдкЉ6ЁмaЃМЉ7ЪБЃЌЭМаЮгыy=aгаШ§ИіНЛЕуЃЌ
Ёрy=aвЊдкЯпЖЮABЕФЯТЗНЃЌ
ЁрaЃМЉ3ЃЌ
ЁрЉ6ЃМaЃМЉ3Лђa=Љ7ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
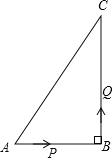
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯBЃН90ЁуЃЌABЃН6cmЃЌBCЃН8cmЃЌЕуPДгAЕуГіЗЂбиABБпЯђBвд1cm/sЕФЫйЖШвЦЖЏЃЌЕуQДгBЕуГіЗЂбиBCЯђCЕувд2cm/sЕФЫйЖШвЦЖЏЃЌЕБЦфжавЛИіЕуЕНДяжеЕуЪБСНИіЕуЭЌЪБЭЃжЙдЫЖЏЃЌдкСНИіЕудЫЖЏЙ§ГЬжаЃЌЧыЛиД№ЃК
ЃЈ1ЃЉОЙ§ЖрЩйЪБМфЃЌЁїPBQЕФУцЛ§ЪЧ5cm2ЃП
ЃЈ2ЃЉЧыФуРћгУХфЗНЗЈЃЌЧѓГіОЙ§ЖрЩйЪБМфЃЌЫФБпаЮAPQCУцЛ§зюаЁЃПВЂЧѓГіетИізюаЁжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮтНЧјФГЭАзАЫЎОгЊВПУПЬьЕФЗПзтЁЂШЫдБЙЄзЪЕШЙЬЖЈГЩБОЮЊ150дЊЃЌУПЭАЫЎЕФНјМлЪЧ5дЊЃЌЙцЖЈЯњЪлЕЅМлВЛЕУИпгк12дЊ/ЭАЃЌвВВЛЕУЕЭгк7дЊ/ЭАЃЌЕїВщЗЂЯжШеОљЯњЪлСП![]() (ЭА)гыЯњЪлЕЅМл
(ЭА)гыЯњЪлЕЅМл![]() (дЊ)ЕФКЏЪ§ЭМЯѓШчЭМЫљЪОЃЎ
(дЊ)ЕФКЏЪ§ЭМЯѓШчЭМЫљЪОЃЎ
ЃЈ1ЃЉЧѓШеОљЯњЪлСП![]() (ЭА)гыЯњЪлЕЅМл
(ЭА)гыЯњЪлЕЅМл![]() (дЊ)ЕФКЏЪ§ЙиЯЕЃЛ
(дЊ)ЕФКЏЪ§ЙиЯЕЃЛ
ЃЈ2ЃЉШєИУОгЊВПЯЃЭћШеОљЛёРћ1200дЊЃЌЧѓИУЭАзАЫЎЕФЯњЪлЕЅМлЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌвЛДЮКЏЪ§y=kx+bЃЈkЁй0ЃЉЕФЭМЯѓгыЗДБШР§КЏЪ§![]() ЃЈmЁй0ЃЉЕФЭМЯѓНЛгкAЁЂBСНЕуЃЌгыxжсНЛгкCЕуЃЌЕуAЕФзјБъЮЊЃЈnЃЌ6ЃЉЃЌЕуCЕФзјБъЮЊЃЈЉ2ЃЌ0ЃЉЃЌЧвtanЁЯACO=2ЃЎ
ЃЈmЁй0ЃЉЕФЭМЯѓНЛгкAЁЂBСНЕуЃЌгыxжсНЛгкCЕуЃЌЕуAЕФзјБъЮЊЃЈnЃЌ6ЃЉЃЌЕуCЕФзјБъЮЊЃЈЉ2ЃЌ0ЃЉЃЌЧвtanЁЯACO=2ЃЎ
ЃЈ1ЃЉЧѓИУЗДБШР§КЏЪ§КЭвЛДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЧѓЕуBЕФзјБъЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПИлжщАФДѓЧХЃЌДг2009ФъПЊЙЄНЈдьЃЌгк2018Фъ10дТ24Шее§ЪНЭЈГЕЃЎЦфШЋГЄ55ЙЋРяЃЌСЌНгИлжщАФШ§ЕиЃЌМЏЧХЁЂЕКЁЂЫэгквЛЬхЃЌЪЧЪРНчЩЯзюГЄЕФПчКЃДѓЧХЃЎШчЭМЪЧИлжщАФДѓЧХЕФКЃырЫўВПЗжаЇЙћЭМЃЌЮЊСЫВтЕУКЃырЫўаБРЫїЖЅЖЫAОрРыКЃЦНУцЕФИпЖШЃЌЯШВтГіаБРЫїЕзЖЫCЕНЧХЫўЕФОрРыЃЈCDЕФГЄЃЉдМЮЊ100УзЃЌгждкCЕуВтЕУAЕуЕФбіНЧЮЊ30ЁуЃЌВтЕУBЕуЕФИЉНЧЮЊ20ЁуЃЌЧѓаБРЫїЖЅЖЫAЕуЕНКЃЦНУцBЕуЕФОрРыЃЈABЕФГЄЃЉЃЎЃЈвбжЊ![]() Ёж1.73ЃЌtan20ЁуЁж0.36ЃЌНсЙћОЋШЗЕН0.1ЃЉ
Ёж1.73ЃЌtan20ЁуЁж0.36ЃЌНсЙћОЋШЗЕН0.1ЃЉ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєxЃНЉmКЭxЃНmЉ4ЪБЃЌЖрЯюЪНax2+bx+4a+1ЕФжЕЯрЕШЃЌЧвmЁй2ЃЎЕБЉ1ЃМxЃМ2ЪБЃЌДцдкxЕФжЕЃЌЪЙЖрЯюЪНax2+bx+4a+1ЕФжЕЮЊ3ЃЌдђaЕФШЁжЕЗЖЮЇЪЧ______ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЯТСаКЏЪ§ЭМЯѓЩЯШЮШЁВЛЭЌСНЕу![]() ЃЌвЛЖЈФмЪЙ
ЃЌвЛЖЈФмЪЙ![]() ГЩСЂЕФЪЧ( )
ГЩСЂЕФЪЧ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
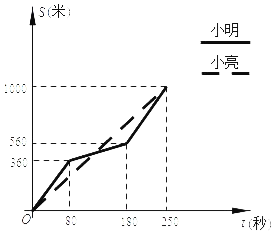
ЁОЬтФПЁПЮЊдіЧПбЇЩњЬхжЪЃЌФГжабЇдкЬхг§ПЮжаМгЧПСЫбЇЩњЕФГЄХмбЕСЗЃЎдквЛДЮФазг1000УзФЭСІВтЪджаЃЌаЁУїКЭаЁССЭЌЪБЦ№ХмЃЌЭЌЪБЕНДяжеЕуЃЛЫљХмЕФТЗГЬSЃЈУзЃЉгыЫљгУЕФЪБМфtЃЈУыЃЉжЎМфЕФКЏЪ§ЭМЯѓШчЭМЫљЪОЃК
ЃЈ1ЃЉЕБ80ЁмtЁм180ЪБЃЌЧѓаЁУїЫљХмЕФТЗГЬSЃЈУзЃЉгыЫљгУЕФЪБМфtЃЈУыЃЉжЎМфЕФКЏЪ§БэДяЪНЃЛ
ЃЈ2ЃЉЧѓЫћУЧЕквЛДЮЯргіЕФЪБМфЪЧЦ№ХмКѓЕФЕкМИУыЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТБэИјГіСЫДњЪ§ЪНax2+bx+cгыxЕФвЛаЉЖдгІжЕЃК
x | Ё | 0 | 1 | 2 | 3 | 4 | Ё |
ax2+bx+c | Ё | 3 | ЁЁ ЁЁ | Љ1 | ЁЁ ЁЁ | 3 | Ё |
ЃЈ1ЃЉЧыдкБэФкЕФПеИёжаЬюШыЪЪЕБЕФЪ§ЃЛ
ЃЈ2ЃЉЩшyЃНax2+bx+cЃЌдђЕБxШЁКЮжЕЪБЃЌyЃМ0ЃЛ
ЃЈ3ЃЉЕБ0ЃМxЃМ3ЃЌЧѓxЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com