
 经过点A(3,0),B(﹣1,0).
经过点A(3,0),B(﹣1,0). 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源:不详 题型:解答题
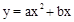 。
。 。
。查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
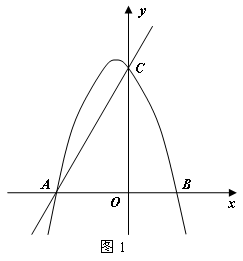
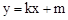 与x轴、y轴分别交于A、C两点,抛物线
与x轴、y轴分别交于A、C两点,抛物线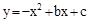 经过A、C两点,点B是抛物线与x轴的另一个交点,当
经过A、C两点,点B是抛物线与x轴的另一个交点,当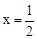 时,y取最大值
时,y取最大值 .
.
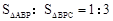 ,求点P的坐标;
,求点P的坐标; 与(1)中所求的抛物线交于M、N两点,问:
与(1)中所求的抛物线交于M、N两点,问: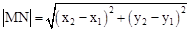 )
)查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 的图象开口向上,图象经过点(-1,2)和(1,0),且与
的图象开口向上,图象经过点(-1,2)和(1,0),且与 轴交于负半轴.给出四个结论:①abc<0;②2a+
轴交于负半轴.给出四个结论:①abc<0;②2a+ >0;③a+c=1; ④a>1.其中正确结论的序号是 (将你认为正确结论的序号都填上) .
>0;③a+c=1; ④a>1.其中正确结论的序号是 (将你认为正确结论的序号都填上) .
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
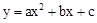 (a≠0)的图象与x轴交于A、B两点,与y轴交于C点,且对称轴为x=1,点B坐标为(﹣1,0).则下面的四个结论:①2a+b=0;②4a-2b+c<0;③ac>0;④当y<0时,x<-1或x>2.其中正确的个数是
(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,且对称轴为x=1,点B坐标为(﹣1,0).则下面的四个结论:①2a+b=0;②4a-2b+c<0;③ac>0;④当y<0时,x<-1或x>2.其中正确的个数是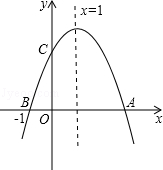
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com