
【题目】如图1,A(﹣2,0),B(0,4),以B点为直角顶点在第二象限作等腰直角△ABC.
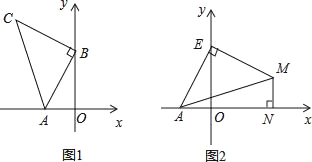
(1)求C点的坐标;
(2)在坐标平面内是否存在一点P,使△PAB与△ABC全等?若存在,求出P点坐标,若不存在,请说明理由;
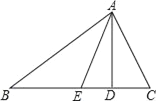
(3)如图2,点E为y轴正半轴上一动点,以E为直角顶点作等腰直角△AEM,过M作MN⊥x轴于N,求OE﹣MN的值.
【答案】(1)C(-4,6);(2)存在,(-6,2)或(2,-2)或(4,2)或(-4,6);(3)2.
【解析】
试题(1)作CE⊥y轴于E,证明△CBE≌△BAO即可得出结论;(2)分为四种情况讨论:①当P和C重合时,△PAB和△ABC全等,即此时P的坐标是(-4,6);②点P在第二象限,过P作PE⊥x轴于E,满足∠PAB=∠AOB=∠PEA=90°,PA=AB,则此时△PAB和△ABC全等,证明△PEA≌△AOB即可得出P点坐标;③点P在第一象限,作∠CAP=90°,交CB的延长线于P,此时△PAB和△ABC全等,过P作PE⊥x轴于E,证明△CMA≌△AEP即可求得P点坐标;④P点在第四象限,作∠BAP=90度,AP=AB,此时△PAB和△ABC全等,证明△AOB≌△PEA即可求出P点坐标;(3)作MF⊥y轴于F,把OE-MN转化成OE-OF,于是OE-MN就等于EF的值,然后证明△AEO≌△EMF,把EF值转化成AO的长度,就求出了OE-MN的结果.
试题解析:(1)作CE⊥y轴于E,如图1,
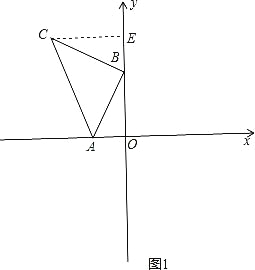
∵A(-2,0),B(0,4),∴OA=2,OB=4,∵∠CBA=90°,∴∠CEB=∠AOB=∠CBA=90°,∴∠ECB+∠EBC=90°∠CBE+∠ABO=90°,∴∠ECB=∠ABO,在△CBE和△BAO中,∠ECB=∠ABO,∠CEB=∠AOB,BC=AB,∴△CBE≌△BAO(AAS),∴CE=BO=4,BE=AO=2,即OE=2+4=6,因为C点在第二象限,∴C(-4,6).
(2)分四种情况讨论:①如图2,当P和C重合时,△PAB和△ABC全等,即此时P的坐标是(-4,6);
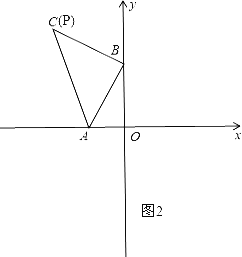
②如图3,点P在第二象限,过P作PE⊥x轴于E,满足∠PAB=∠AOB=∠PEA=90°,PA=AB,则此时△PAB和△ABC全等,∵∠EPA+∠PAE=90°,∠PAE+∠BAO=90°,∴∠EPA=∠BAO(同角的余角相等),在△PEA和△AOB中,∠EPA=∠BAO,∠PEA=∠AOB,PA=AB,∴△PEA≌△AOB,∴PE=AO=2,EA=BO=4,∴OE=2+4=6,即P的坐标是(-6,2);
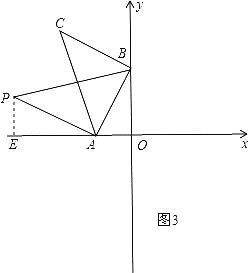
③如图4,点P在第一象限,作∠CAP=90°,交CB的延长线于P,此时△PAB和△ABC全等,过P作PE⊥x轴于E,过C作CM⊥x轴于M,
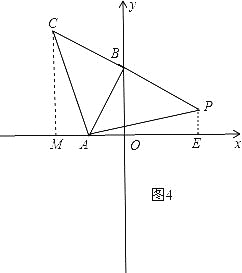
则∠CMA=∠PEA=90°,∵△CBA≌△PBA,∴∠PAB=∠CAB=45°,AC=AP,∴∠CAP=90°,∴∠MCA+∠CAM=90°,∠CAM+∠PAE=90°,∴∠MCA=∠PAE,在△CMA和△AEP中,∠MCA=∠PAE,∠CMA=∠PEA,AC=AP,∴△CMA≌△AEP,∴PE=AM,CM=AE,∵C(-4,6),A(-2,0),
∴PE=AM=4-2=2,OE=AE-A0=6-2=4,即P的坐标是(4,2);
④如图5,P点在第四象限,作∠BAP=90度,AP=AB,此时△PAB和△ABC全等,过P作PE⊥x轴于E,
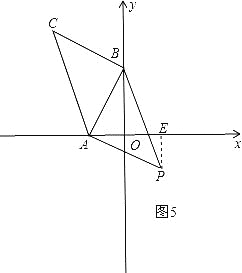
∵△CBA≌△PAB,∴AB=AP,∠CBA=∠BAP=90°,则∠AEP=∠AOB=90°,∴∠BAO+∠PAE=90°,∠PAE+∠APE=90°,∴∠BAO=∠APE,在△AOB和△PEA中,∠BAO=∠APE,∠AOB=∠PEA,AB=AP,∴△AOB≌△PEA,∴PE=AO=2,AE=OB=4,∴0E=AE-AO=4-2=2,即P的坐标是(2,-2).综上所述:坐标平面内存在一点P,使△PAB与△ABC全等,符合条件的P的坐标是(-6,2)或(2,-2)或(4,2)或(-4,6).(3)如图6,作MF⊥y轴于F,

则∠AEM=∠EFM=∠AOE=90°,∵∠AEO+∠MEF=90°,∠MEF+∠EMF=90°,∴∠AEO=∠EMF,在△AOE和△EMF中,∠AOE=∠EFM,∠AEO=∠EMF,AE=EM,∴△AEO≌△EMF,∴EF=AO=2,MF=OE,∵MN⊥x轴,MF⊥y轴,∴∠MFO=∠FON=∠MNO=90°,∴四边形FONM是矩形,∴MN=OF,∴OE-MN=OE-OF=EF=OA=2.即OE-MN的值是2.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
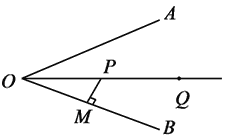
【题目】已知:BOA是一条公路,河流OP恰好经过桥O平分∠AOB.
(1)如果要从P处移动到公路上路径最短,除图中所示PM外,还可以选择PN,求作这条路径,两条路径的关系是______,理由是___________.
(2)河流下游处有一点Q,如果要从P点出发,到达公路OA上的点C后再前往点Q,请你画出一条最短路径,表明点C的位置.
(3)D点在公路OB上,O点到D点的距离与C点相等,作出△CDP,求证:△CDP为等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题情境】
已知矩形的面积为a(a为常数,a>0),当该矩形的长为多少时,它的周长
最小?最小值是多少?
【数学模型】
设该矩形的长为x,周长为y,则y与x的函数表达式为y=2(x+ ![]() )(x>0).
)(x>0).
【探索研究】
小彬借鉴以前研究函数的经验,先探索函数y=x+ ![]() 的图象性质.
的图象性质.
(1)结合问题情境,函数y=x+ ![]() 的自变量x的取值范围是x>0,如表是y与x的几组对应值.
的自变量x的取值范围是x>0,如表是y与x的几组对应值.
x | … |
|
|
| 1 | 2 | 3 | m | … |
y | … | 4 | 3 | 2 | 2 | 2 | 3 | 4 | … |
①写出m的值;
②画出该函数图象,结合图象,得出当x=时,y有最小值,y最小=;
(2)【解决问题】
直接写出“问题情境”中问题的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD、AE分别是△ABC的高和角平分线,∠B=30°,∠C=70°,分别求:
(1)∠BAC的度数;
(2)∠AED的度数;
(3)∠EAD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形![]() 中,
中,![]() =4cm,
=4cm,![]() =3cm,
=3cm,![]() 为
为![]() 的中点.动点
的中点.动点![]() 从
从![]() 点出发,以每秒1cm的速度沿
点出发,以每秒1cm的速度沿![]() 运动,最终到达点
运动,最终到达点![]() .若点
.若点![]() 运动的时间为
运动的时间为![]() 秒,则当
秒,则当![]() =________ 时,
=________ 时,![]() 的面积等于4.5.
的面积等于4.5.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E,F.

(1)求证:DE=DF;
(2)若∠A=60°,BE=1,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设平面内一点到等边三角形中心的距离为d,等边三角形的内切圆半径为r,外接圆半径为R.对于一个点与等边三角形,给出如下定义:满足r≤d≤R的点叫做等边三角形的中心关联点. 在平面直角坐标系xOy中,等边△ABC的三个顶点的坐标分别为A(0,2),B(﹣ ![]() ,﹣1),C(
,﹣1),C( ![]() ,﹣1).
,﹣1).
(1)已知点D(2,2),E( ![]() ,1),F(﹣
,1),F(﹣ ![]() ,﹣1).在D,E,F中,是等边△ABC的中心关联点的是;
,﹣1).在D,E,F中,是等边△ABC的中心关联点的是;
(2)如图1,过点A作直线交x轴正半轴于M,使∠AMO=30°. ①若线段AM上存在等边△ABC的中心关联点P(m,n),求m的取值范围;
②将直线AM向下平移得到直线y=kx+b,当b满足什么条件时,直线y=kx+b上总存在等边△ABC的中心关联点;(直接写出答案,不需过程)
(3)如图2,点Q为直线y=﹣1上一动点,⊙Q的半径为 ![]() .当Q从点(﹣4,﹣1)出发,以每秒1个单位的速度向右移动,运动时间为t秒.是否存在某一时刻t,使得⊙Q上所有点都是等边△ABC的中心关联点?如果存在,请直接写出所有符合题意的t的值;如果不存在,请说明理由.
.当Q从点(﹣4,﹣1)出发,以每秒1个单位的速度向右移动,运动时间为t秒.是否存在某一时刻t,使得⊙Q上所有点都是等边△ABC的中心关联点?如果存在,请直接写出所有符合题意的t的值;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张庄甲、乙两家草莓采摘园的草莓销售价格相同,“春节期间”,两家采摘园将推出优惠方案,甲园的优惠方案是:游客进园需购买门票,采摘的草莓六折优惠;乙园的优惠方案是:游客进园不需购买门票,采摘园的草莓超过一定数量后,超过部分打折优惠.优惠期间,某游客的草莓采摘量为![]() (千克),在甲园所需总费用为
(千克),在甲园所需总费用为![]() (元),在乙园所需总费用为
(元),在乙园所需总费用为![]() (元),
(元),![]() 、
、![]() 与
与![]() 之间的函数关系如图所示,折线OAB表示
之间的函数关系如图所示,折线OAB表示![]() 与
与![]() 之间的函数关系.
之间的函数关系.

(1)甲采摘园的门票是 元,两个采摘园优惠前的草莓单价是每千克 元;
(2)当![]() >10时,求
>10时,求![]() 与
与![]() 的函数表达式;
的函数表达式;
(3)游客在“春节期间”采摘多少千克草莓时,甲、乙两家采摘园的总费用相同.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com