
【题目】如图,M、N分别是正方形ABCD边DC、AB的中点,分别以AE、BF为折痕,使点D、点C落在MN的点G处,则△ABG是 三角形.
【答案】等边
【解析】解:由折叠的性质可知AG=AD,BG=BC,
∵四边形ABCD是正方形,
∴AD=AB=BC.
∴AG=AB=BG.
∴△ABG是等边三角形.
所以答案是:等边.
【考点精析】本题主要考查了等边三角形的判定和正方形的性质的相关知识点,需要掌握三个角都相等的三角形是等边三角形;有一个角等于60°的等腰三角形是等边三角形;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能正确解答此题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】若正整数k满足个位数字为1,其他数位上的数字均不为1且十位与百位上的数字相等,
我们称这样的数k为“言唯一数”,交换其首位与个位的数字得到一个新数k',并记F(k)=![]() .
.
(1)最大的四位“言唯一数”是 ,最小的三位“言唯一数”是 ;
(2)证明:对于任意的四位“言唯一数”m,m+m'能被11整除;
(3)设四位“言唯一数”n=1000x+100y+10y+1(2≤x≤9,0≤y≤9且y≠1,x、y均为整数),若F(n)仍然为“言唯一数”,求所有满足条件的四位“言唯一数”n.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车厂去年每个季度汽车销售数量(辆)占当季汽车产量(辆)百分比的统计图如图所示.根据统计图回答下列问题: 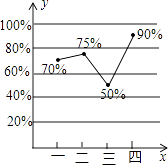
(1)若第一季度的汽车销售量为2100辆,求该季的汽车产量;
(2)圆圆同学说:“因为第二,第三这两个季度汽车销售数量占当季汽车产量是从75%降到50%,所以第二季度的汽车产量一定高于第三季度的汽车产量”,你觉得圆圆说的对吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,利用尺规,根据下列要求作图(保留作图痕迹,不写作法),并根据要求填空:
(1)作∠ABC的平分线BD交AC于点D;
(2)作BD的垂直平分线交AB于E,交BC于F;
(3)在(1)、(2)条件下,连接DE,线段DE与线段BF的关系为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定两数a、b之间的一种运算,记作(a,b):如果![]() ,那么(a,b)=c.
,那么(a,b)=c.
例如:因为![]() ,所以(2,8)=3.
,所以(2,8)=3.
(1)根据上述规定,填空:
(5,125)= ,(-2,4)= ,(-2,-8)= ;
(2)小明在研究这种运算时发现一个现象:![]() ,他给出了如下的证明:
,他给出了如下的证明:
设![]() ,则
,则![]() ,即
,即![]()
∴![]() ,即
,即![]() ,
,
∴![]() .
.
请你尝试运用上述这种方法说明下面这个等式成立的理由.
(4,5)+(4,6)=(4,30)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以∠AOB的顶点O为圆心,适当长为半径画弧,交OA于点C,交OB于点D,再分别以点C、D为圆心,大于![]() CD的长为半径画弧,两弧在∠AOB内部交于点E,作射线OE,连接CD.以下说法错误的是( )
CD的长为半径画弧,两弧在∠AOB内部交于点E,作射线OE,连接CD.以下说法错误的是( )

A. △OCD是等腰三角形 B. 点E到OA、OB的距离相等
C. CD垂直平分OE D. 证明射线OE是角平分线的依据是SSS
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班毕业联欢会设计的即兴表演节目的摸球游戏,游戏采用一个不透明的盒子,里面装有五个分别标有数字1、2、3、4、5的乒乓球,这些球除数字外,其它完全相同,游戏规则是参加联欢会的50名同学,每人将盒子乒乓球摇匀后闭上眼睛从中随机一次摸出两个球(每位同学必须且只能摸一次).若两球上的数字之和是偶数就给大家即兴表演一个节目;否则,下个同学接着做摸球游戏,依次进行.
(1)用列表法或画树状图法求参加联欢会同学表演即兴节目的概率;
(2)估计本次联欢会上有多少个同学表演即兴节目.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com