
【题目】请阅读下列材料:
问题:如图(1),一圆柱的高为5dm,底面半径为5dm,BC是底面直径,求一只蚂蚁从A点出发沿圆柱表面爬行到点C的最短路线.小明设计了两条路线:
路线1:侧面展开图中的AC.如下图(2)所示:
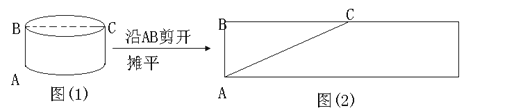
设路线1的长度为![]() ,则
,则![]() ,
,
路线2:高线AB + 底面直径BC.如上图(1)所示:
设路线2的长度为![]() ,则
,则![]() ,
,
∵![]() ,
,
∴![]()
∴![]() ,
,
所以要选择路线2较短.
(1)小明对上述结论有些疑惑,于是他把条件改成:“圆柱的底面半径为1dm,高AB为5dm”继续按前面的路线进行计算.请你帮小明完成下面的计算:
路线1:![]() ___________________;
___________________;
路线2:![]() __________
__________
∵![]()
![]() ,
,
∴![]()
![]() (填>或<) 所以应选择路线_________(填1或2)较短.
(填>或<) 所以应选择路线_________(填1或2)较短.
(2)请你帮小明继续研究:在一般情况下,当圆柱的底面半径为r,高为h时,应如何选择上面的两条路线才能使蚂蚁从点A出发沿圆柱表面爬行到C点的路线最短.
【答案】(1)25+π2;49;<;<;1;(2)(2)当r<![]() ,l1<l2;当r=
,l1<l2;当r=![]() ,l1=l2;当r>
,l1=l2;当r>![]() ,l1>l2.
,l1>l2.
【解析】
(1)根据勾股定理易得路线1:l12=AC2=高2+底面周长一半2;路线2:l22=(高+底面直径)2,然后比较即可;
(2)先分别求出l12和l22的值,进而得出l12-l22的值,然后分三种情况计算即可.
解:(1)路线1:l12=AC2=25+π2;
路线2:l22=(AB+BC)2=49.
∵l12<l22,
∴l1<l2,
∴选择路线1较短.
故答案为:25+π2;49;<;<;1;
(2)l12=AC2=AB2+BC2=h2+(πr)2,
l22=(AB+BC)2=(h+2r)2,
∴l12-l22=h2+(πr)2-(h+2r)2=r(π2r-4r-4h)=r[(π2-4)r-4h],
当r[(π2-4)r-4h]<0时,r<![]() ,此时l12<l22,即l1<l2;
,此时l12<l22,即l1<l2;
当r[(π2-4)r-4h]=0时,r=![]() ,此时l12=l22,即l1=l2;
,此时l12=l22,即l1=l2;
当r[(π2-4)r-4h]>0时,r>![]() ,此时l12>l22,即l1>l2;
,此时l12>l22,即l1>l2;
综上可知:当r<![]() ,l1<l2;当r=
,l1<l2;当r=![]() ,l1=l2;当r>
,l1=l2;当r>![]() ,l1>l2.
,l1>l2.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某学校为了增强学生体质,决定开设以下体育课外活动项目:A:篮球 B:乒乓球C:羽毛球 D:足球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:


(1)这次被调查的学生共有 人;
(2)请你将条形统计图(2)补充完整;
(3)在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,D是BC的中点,连接AD,E为AD的中点,过A作AF∥BC交BE延长线于F,连接CF.
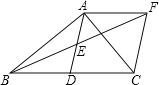
(1)求证:四边形ADCF是菱形;
(2)在不添加任何辅助线的情况下,请直接写出与△ACD面积相等的三角形(不包含△ACD).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A的坐标为(4,0),点B的坐标为(10,0),点C为平面上一动点,连接CA,CB,将线段CB绕点C逆时针旋转90°得到线段CD,当AC=4,线段AD的长取最大值时,点D的坐标为_____.
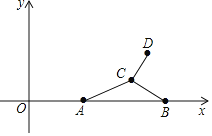
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,点E是CD上一点(不与C,D两点重合),连接BE,过点C作CH⊥BE于点F,交对角线BD于点G,交AD边于点H,连接GE,
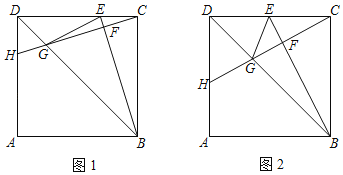
(1)求证:△DHC≌△CEB;
(2)如图2,若点E是CD的中点,当BE=8时,求线段GH的长;
(3)设正方形ABCD的面积为S1,四边形DEGH的面积为S2,当![]() 的值为
的值为![]() 时,
时,![]() 的值为 .
的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年3月2日,500架无人飞机在西安创业咖啡街区的夜空绽放,西安高新区用“硬科技”打造了最具独特的风景线,2018“西安年,最中国”以一场华丽的视觉盛宴完美收官,当晚,某兴趣爱好者想用手中的无人机测量大雁塔的高度,如图是从大雁塔正南面看到的正视图,兴趣爱好者将无人机上升至离地面185米高大雁塔正东面的F点,此时,他测得F点都塔顶A点的俯视角为30°,同时也测得F点到塔底C点的俯视角为45°,已知塔底边心距OC=23米,请你帮助该无人机爱好者计算出大雁塔的大体高度(结果精确到0.1米)?(![]() ≈1.73,
≈1.73,![]() ≈1.41).
≈1.41).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的布袋中装有相同的三个小球,其上面分别标注数字1、2、3、,现从中任意摸出一个小球,将其上面的数字作为点M的横坐标;将球放回袋中搅匀,再从中任意摸出一个小球,将其上面的数字作为点M的纵坐标.
(1)求点M在直线y=x上的概率;
(2)求点M的横坐标与纵坐标之和是偶数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
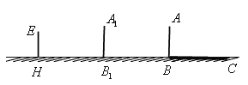
【题目】学习投影后,小明、小颖利用灯光下自己的影子长度来测量一路灯的高度,并探究影子长度的变化规律.如图,在同一时间,身高为![]() 的小明
的小明![]() 的影子
的影子![]() 长是
长是![]() ,而小颖
,而小颖![]() 刚好在路灯灯泡的正下方
刚好在路灯灯泡的正下方![]() 点,并测得
点,并测得![]() .
.
(1)请在图中画出形成影子的光线,并确定路灯灯泡所在的位置![]() ;
;
(2)求路灯灯泡的垂直高度![]() ;
;
(3)如果小明沿线段BH向小颖(点H)走去,当小明走到BH中点B1处时,请在图中画出此时小明的影长B1C1,并求B1C1的长;
查看答案和解析>>
科目:初中数学 来源: 题型:
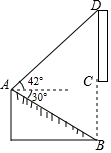
【题目】小婷在放学路上,看到隧道上方有一块宣传“中国﹣南亚博览会”的竖直标语牌CD.她在A点测得标语牌顶端D处的仰角为42°,测得隧道底端B处的俯角为30°(B,C,D在同一条直线上),AB=10m,隧道高6.5m(即BC=65m),求标语牌CD的长(结果保留小数点后一位).(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90,![]() ≈1.73)
≈1.73)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com