练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    反比例函数y=﹣的图象上有P1（x1，﹣2），P2（x2，﹣3）两点，则x1与x2的大小关系是（　　）

    A. x1＞x2 B. x1=x2 C. x1＜x2 D. 不确定

    A 【解析】∵反比例函数y=?的图象上有 (,?2), (,?3)两点， ∴每个分支上y随x的增大而增大，∵?2>?3，∴>， 故选：A.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：云南省双柏县2017-2018学年上学期七年级期末数学试卷 题型：填空题

    多项式4a-b2的次数是__________________．

    2 【解析】【解析】 多项式4a-b2的次数是2．故答案为：2．

    查看答案和解析>>

    科目：初中数学 来源：江苏省南京市联合体2018届九年级上学期期末考试数学试卷 题型：填空题

    若一个圆锥的侧面展开图是一个半径为3cm，圆心角为120°的扇形，则该圆锥的侧面面积为_____cm2（结果保留π）．

    3π 【解析】.

    查看答案和解析>>

    科目：初中数学 来源：山东省东营市河口区2017-2018学年度第一学期期末考试九年级数学试卷 题型：解答题

    （1）计算： ；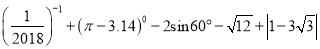

    （2）先化简，再求值： ，其中x=4﹣tan45°．

    (1)2018；（2）. 【解析】试题分析：（1）根据负整数指数幂，零指数幂的定义，特殊角的三角函数值，二次根式的性质，绝对值的意义化简计算即可； （2）先用分式的混合运算法则化简分式，然后代入求值即可． 试题解析：【解析】 （1）原式==2018； （2）原式=== 当x=4﹣tan45°=4－1=3时，原式=．

    查看答案和解析>>

    科目：初中数学 来源：山东省东营市河口区2017-2018学年度第一学期期末考试九年级数学试卷 题型：填空题

    在Rt△ABC中，∠C=90°，若sinA=，则cosB的值是____________ ．

    【解析】试题分析：如图： 在Rt△ABC中，∠C=90°．因为sinA=，不妨设BC=3k，AB=5k，cosB=

    查看答案和解析>>

    科目：初中数学 来源：山东省东营市河口区2017-2018学年度第一学期期末考试九年级数学试卷 题型：单选题

    已知关于x的方程x2+3x+a=0有一个根为﹣2，则另一个根为（　　）

    A. 5 B. ﹣1 C. 2 D. ﹣5

    B 【解析】根据一元二次方程根与系数的关系，利用两根和，两根积，即可求出a的值和另一根． 【解析】 设一元二次方程的另一根为x1， 则根据一元二次方程根与系数的关系， 得﹣2+x1=﹣3， 解得：x1=﹣1． 故选B．

    查看答案和解析>>

    科目：初中数学 来源：北京大学附属中学2017-2018学年七年级上学期期中考试数学试卷 题型：解答题

    解方程：

    （）．

    （）．

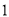    （1）（2）x=3 【解析】试题分析：先去括号，然后移项合并，最后化系数为1即可得出方程的解． 试题解析：（） ∴． （） ∴．

    查看答案和解析>>

    科目：初中数学 来源：北京大学附属中学2017-2018学年七年级上学期期中考试数学试卷 题型：单选题

    下列各式中，去括号正确的是（ ）．

    A. B.

    C. D.

    C 【解析】试题解析： 、，错误； 、，错误； 、，正确； 、，错误； 故选C.

    查看答案和解析>>

    科目：初中数学 来源：江苏省东部分校2017-2018学年八年级上学期期末考试数学试卷 题型：解答题

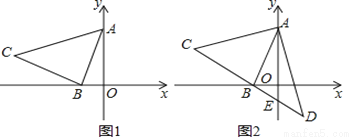
    如图1，已知直线y=2x+2与y轴、x轴分别交于A、B两点，以B为直角顶点在第二象限作等腰Rt△ABC ．

    （1）求点C的坐标，并求出直线AC的关系式．

    （2）如图2，直线CB交y轴于E，在直线CB上取一点D，连接AD，若AD=AC，求证：BE=DE．

    （3）如图3，在（1）的条件下，直线AC交x轴于M，P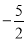（，k）是线段BC上一点，在线段BM上是否存在一点N，使△BPN的面积等于△BCM面积的？若存在，请求出点N的坐标；若不存在，请说明理由．

    （1）C（﹣3，1），直线AC：y=x+2；（2）证明见解析；（3）N（﹣，0）． 【解析】试题分析：（1）作CQ⊥x轴，垂足为Q，根据条件证明△ABO≌△BCQ，从而求出CQ=OB=1，可得C（﹣3，1），用待定系数法可求直线AC的解析式y=x+2；（2）作CH⊥x轴于H，DF⊥x轴于F，DG⊥y轴于G，证明△BCH≌△BDF，△BOE≌△DGE，可得BE=DE；（3）先求出直线BC的解析...

    查看答案和解析>>

    同步练习册答案