
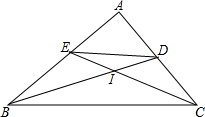
 已知:Rt△ABC,∠A为直角,I为内心,BD,CE分别为两内角平分线,△IBC的面积为S,求四边形BCDE的面积.
已知:Rt△ABC,∠A为直角,I为内心,BD,CE分别为两内角平分线,△IBC的面积为S,求四边形BCDE的面积. 分析 在BC上截取BM=BE、CN=CD,根据SAS定理可以证明△BIE≌△BIM,△CID≌△CIN,再根据全等三角形对应边相等得到EI=MI,DI=NI,全等三角形对应角相等,推出∠EID与∠MIN互补,从而得到△DIE与△MIN的面积相等,最后求出四边形BCDE的面积等于△BIC的面积的2倍.
解答 解:如图,在BC上截取BM=BE、CN=CD,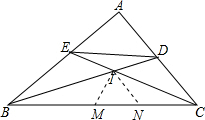
∵BD,CE分别为两内角平分线,
则△BIE≌△BIM(SAS),△CID≌△CIN(SAS),
∵∠BIM=∠BIE=45°,∠CIN=∠CID=45°,
即∠EIM=∠DIN=90°,
∴∠DIE+∠MIN=180°,
∴S△DIE=S△MIN,
∴S四边形BCDE=2S△BCI=2S.
点评 本题主要考查了三角形内心的性质和全等三角形的判定与性质,读懂题目信息是解题的关键,根据信息作辅助线构造出符合信息的图形是本题的难点.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
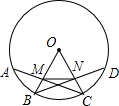 如图,在⊙O中,$\widehat{AB}=\widehat{BC}=\widehat{CD}$,半径OB,OC分别交弦AC,BD于点M,N,求证:∠OMN=∠ONM.
如图,在⊙O中,$\widehat{AB}=\widehat{BC}=\widehat{CD}$,半径OB,OC分别交弦AC,BD于点M,N,求证:∠OMN=∠ONM.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
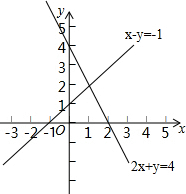 直线x-y=-1与直线2x+y=4在同一平面直角坐标系中的位置如图所示,请你在图中标出这两条直线的交点坐标,写出二元一次方程组$\left\{\begin{array}{l}{x-y=-1}\\{2x+y=4}\end{array}\right.$的解$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$.
直线x-y=-1与直线2x+y=4在同一平面直角坐标系中的位置如图所示,请你在图中标出这两条直线的交点坐标,写出二元一次方程组$\left\{\begin{array}{l}{x-y=-1}\\{2x+y=4}\end{array}\right.$的解$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3个 | B. | 4个 | C. | 16个 | D. | 64个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 课堂发言次数n | |
| A | 0≤n<5 |
| B | 5≤n<10 |
| C | 10≤n<15 |
| D | 15≤n<20 |
| E | 20≤n<25 |
| F | 25≤n<30 |
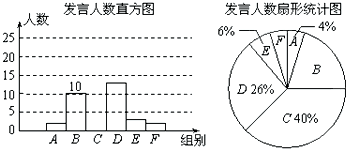
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC的周长为18cm,BE、CF分别为AC、AB边的中线,BE、CF相交于点O,AO的延长线交BC于D,且AF=3cm,AE=2cm,S△ABC=36cm2.
如图,△ABC的周长为18cm,BE、CF分别为AC、AB边的中线,BE、CF相交于点O,AO的延长线交BC于D,且AF=3cm,AE=2cm,S△ABC=36cm2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com