
【题目】如图,等边三角形![]() 的边长为4,点
的边长为4,点![]() 是△ABC的中心,
是△ABC的中心,![]() ,
,![]() 的两边
的两边![]() 与
与![]() 分别相交于
分别相交于![]() ,
,![]() 绕
绕![]() 点顺时针旋转时,下列四个结论正确的个数是( )
点顺时针旋转时,下列四个结论正确的个数是( )
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 周长最小值是9.
周长最小值是9.

A.1个B.2个C.3个D.4个
【答案】B
【解析】
首先连接OB、OC,如图,利用等边三角形的性质得∠ABO=∠OBC=∠OCB=30°,再证明∠BOD=∠COE,于是可判断△BOD≌△COE,利用全等三角形的对应边相等可对①进行判断;再利用S![]() =S
=S![]() 得到四边形ODBE的面积=
得到四边形ODBE的面积=![]() S
S![]() ,则可对③进行判断,然后作OH⊥DE,则DH=EH,计算出S
,则可对③进行判断,然后作OH⊥DE,则DH=EH,计算出S![]() =
=![]() OE
OE![]() ,利用S△ODE随OE的变化而变化和四边形ODBE的面积为定值可对②进行判断,
,利用S△ODE随OE的变化而变化和四边形ODBE的面积为定值可对②进行判断,
接下来由△BDE的周长=BC+DE=4+DE=4+![]() OE,结合垂线段最短,当OE⊥BC时,OE最小,△BDE的周长最小,计算出此时OE的长则可对④进行判断.
OE,结合垂线段最短,当OE⊥BC时,OE最小,△BDE的周长最小,计算出此时OE的长则可对④进行判断.
连接OB,OC,如图.
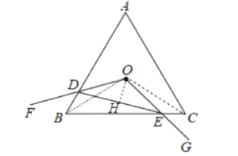
∵△ABC为等边三角形,
∴∠ABC=∠ACB=60°.
∵点O是△ABC的中心,
∴OB=OC,OB. OC分别平分∠ABC和∠ACB,
∴∠ABO=∠OBC=∠OCB=30°,
∴∠BOC=120°,即∠BOE+∠COE=120°,
而∠DOE=120°,即∠BOE+∠BOD=120°,
∴∠BOD=∠COE.
在△BOD和△COE中,∠BOD=∠COE,BO=CO,∠OBD=∠OCE,
∴△BOD≌△COE,
∴BD=CE,OD=OE,所以①正确;
∴S![]() =S
=S![]() ,
,
∴四边形ODBE的面积=S![]() =
=![]() S
S![]() =
=![]() ×
×![]() ×4
×4![]() =
=![]() ,所以③正确;
,所以③正确;
作OH⊥DE,如图,则DH=EH,
∵∠DOE=120°,
∴∠ODE=∠OEH=30°.
∴OH=![]() OE,HE=
OE,HE=![]() OH=
OH=![]() OE,
OE,
∴DE=![]() OE,
OE,
∴S△ODE=![]() ·
·![]() ·OE·
·OE·![]() OE=
OE=![]() OE
OE![]() ,
,
即S![]() 随OE的变化而变化,而四边形ODBE的面积为定值,
随OE的变化而变化,而四边形ODBE的面积为定值,
∴S![]() ≠S
≠S![]() ,所以②错误;
,所以②错误;
∵BD=CE,
∴△BDE的周长=BD+BE+DE=CE+BE+DE=BC+DE=4+DE=4+![]() OE,
OE,
当OE⊥BC时,OE最小,△BDE的周长最小,此时OE=![]() ,
,
∴△BDE周长的最小值=4+2=6,所以④错误.
故选:B.


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:
【题目】如图是用长度相等的小棒按一定规律摆成的一组图案
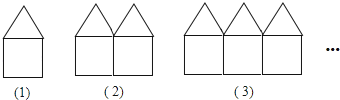
(1)填写下表:
图形序号 | ① | ② | ③ | …… | ⑧ |
每个图案中小棒的数量 | 6 | 11 | …… |
(2)请填写出第![]() 个图案中小棒的数量(用含
个图案中小棒的数量(用含![]() 的代数式表示);
的代数式表示);
(3)第30个图案中小棒有多少根?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一位农民带上若干千克自产的苹果进城出售.为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出的苹果![]() (千克)与他手中持有的钱数
(千克)与他手中持有的钱数![]() (元)(含备用零钱)的关系如图,结合图象解决下列问题:
(元)(含备用零钱)的关系如图,结合图象解决下列问题:
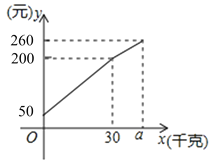
(1)农民自带的零钱是多少?
(2)求出降价前每千克的苹果价格是多少?
(3)降价后他按每千克![]() 元将剩余苹果售完,这时他手中
元将剩余苹果售完,这时他手中![]() 的钱(含备用零钱)是
的钱(含备用零钱)是![]() 元,试求出图象中
元,试求出图象中![]() 的值;
的值;
(4)求出降价前![]() 与
与![]() 之间的关系式(不要求写
之间的关系式(不要求写![]() 的取值范围).
的取值范围).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() O
O![]() 中,正方形A1B1C1O、A2B2C2B1、A3B3C3B2,…, 按图所示的方式放置.点A1、A2、A3,…和点B1、B2、B3,…分别在直线
中,正方形A1B1C1O、A2B2C2B1、A3B3C3B2,…, 按图所示的方式放置.点A1、A2、A3,…和点B1、B2、B3,…分别在直线![]() 和
和![]() 轴上.已知C1(1,-1),C2(
轴上.已知C1(1,-1),C2(![]() ,
, ![]() ),则点A3的坐标是________________________.
),则点A3的坐标是________________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系xOy中,O是坐标原点,以P(1,1)为圆心的⊙P与x轴、y轴分别相切于点M和点N,点F从点M出发,沿x轴正方向以每秒1个单位长度的速度运动,连接PF,过点P作PE⊥PF交y轴于点E,设点F运动的时间是t秒(t>0)
(1)若点E在y轴的负半轴上(如图所示),求证:PE=PF;
(2)在点F运动过程中,设OE=a,OF=b,试用含a的代数式表示b;
(3)作点F关于点M的对称点F′,经过M、E和F′三点的抛物线的对称轴交x轴于点Q,连接QE.在点F运动过程中,是否存在某一时刻,使得以点Q、O、E为顶点的三角形与以点P、M、F为顶点的三角形相似?若存在,请直接写出t的值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小华在晚上由路灯A走向路灯B.当他走到点P时,发现他身后影子的顶部刚好接触到路灯A的底部;当他向前再步行12m到达点Q时,发现他身前影子的顶部刚好接触到路灯B的底部.已知小华的身高是1.6m,两个路灯的高度都是9.6m,且AP=QB.
(1)求两个路灯之间的距离;
(2)当小华走到路灯B的底部时,他在路灯A下的影长是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com