
(10分)已知△ABC是边长为6cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC匀速运动,其中点P运动的速度是1cm/s,点Q运动的速度是2cm/s,当点Q到达点C时,P、Q两点都停止运动,设运动时间为t(s),解答下列问题:
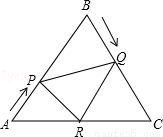
(1)当t=2时,判断△BPQ的形状,并说明理由;
(2)设△BPQ的面积为S(cm2),求S与t的函数关系式;
(3)作QR∥BA交AC于点R,连接PR,当t为何值时,△APR∽△PRQ.
(1)等边三角形;(2)S=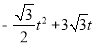 ;(3)t=
;(3)t=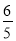 .
.
【解析】
试题分析:(1)当t=2时,分别求出BQ和BP的长度,然后进行说明;(2)过点Q作QE⊥AB,利用三角函数求出QE的长度,然后求出△BPQ与t之间的关系;(3)根据题意可得△CRQ为等边三角形,求出QR、BE、EP与t的关系可以得出四边形EPQR是平行四边形,然后进行计算.
试题解析:(1)△BPQ是等边三角形
当t=2时 AP=2×1=2,BQ=2×2=4
∴BP=AB﹣AP=6﹣2=4 ∴BQ=BP 又∵∠B=60°
∴△BPQ是等边三角形;
(2)过Q作QE⊥AB,垂足为E
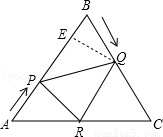
由QB=2t,得QE=2t•sin60°= t 由AP=t,得PB=6﹣t
t 由AP=t,得PB=6﹣t
∴S△BPQ=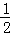 ×BP×QE=
×BP×QE=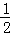 (6﹣t)×
(6﹣t)×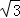 t=﹣
t=﹣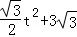 t
t
∴S=﹣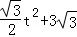 t;
t;
(3)∵QR∥BA ∴∠QRC=∠A=60°,∠RQC=∠B=60°
∴△QRC是等边三角形 ∴QR=RC=QC=6﹣2t
∵BE=BQ•cos60°= ×2t=t
×2t=t
∴EP=AB﹣AP﹣BE=6﹣t﹣t=6﹣2t
∴EP∥QR,EP=QR ∴四边形EPRQ是平行四边形
∴PR=EQ=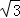 t 又∵∠PEQ=90°, ∴∠APR=∠PRQ=90° ∵△APR∽△PRQ,
t 又∵∠PEQ=90°, ∴∠APR=∠PRQ=90° ∵△APR∽△PRQ,
∴∠QPR=∠A=60° ∴tan60°=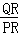 即
即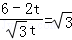 解得t=
解得t=
∴当t= 时,△APR∽△PRQ.
时,△APR∽△PRQ.
考点:二次函数的实际应用、三角形相似的判定.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2014-2015学年江苏省盐城市阜宁县八年级上学期期中调研数学试卷(解析版) 题型:解答题
(4分)如图:已知∠AOB和C、D两点,求作一点P,使PC=PD,且P到∠AOB两边的距离相等.(保留作图痕迹,不写作法)

查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省金华市青春共同体九年级上学期期中考试数学试卷(解析版) 题型:选择题
下列命题中,正确的是( )
①顶点在圆周上的角是圆周角;②圆周角的度数等于圆心角度数的一半;③90°的圆周角所对的弦是直径;④不在同一条直线上的三个点确定一个圆;⑤同弧所对的圆周角相等
A.①②③ B.③④⑤ C.①②⑤ D.②④⑤
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省潍坊地区九年级上学期期末质量评估数学试卷(解析版) 题型:选择题
已知反比例函数y=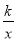 的图像经过点P(-1,2),则这个函数图像位于( )
的图像经过点P(-1,2),则这个函数图像位于( )
A.第二、三象限 B.第一、三象限
C.第三、四象限 D.第二、四象限
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省潍坊地区九年级上学期期末质量评估数学试卷(解析版) 题型:选择题
下列命题中的假命题是( )
A.正方形的半径等于正方形的边心距的 倍
倍
B.三角形任意两边的垂直平分线的交点是三角形的外心
C.用反证法证明命题“三角形中至少有一个内角不小于60°”时,第一步应该“假设每一个内角都小于60°”
D.过三点能且只能作一个圆
查看答案和解析>>
科目:初中数学 来源:2014-2015学年河南省南阳市九年级上期期末摸底数学试卷(解析版) 题型:解答题
(9分)先化简,再求值.(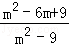 ﹣
﹣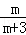 )÷
)÷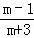 ,其中m=tan45°+2cos30°.
,其中m=tan45°+2cos30°.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年河南省南阳市九年级上期期末摸底数学试卷(解析版) 题型:填空题
已知一元二次方程有一个根是2,那么这个方程可以是_________(填上一个符合条件的方程即可答案不惟一).
查看答案和解析>>
科目:初中数学 来源:2014-2015学年甘肃省白银市会宁县九年级上学期期末考试数学试卷(解析版) 题型:解答题
下图是一个立体图形的三视图,请根据视图写出该立体图形的名称,并计算该立体图形的体积(结果保留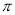 ).
).

查看答案和解析>>
科目:初中数学 来源:2013-2014学年内蒙古包头市九年级上学期期末考试数学试卷(解析版) 题型:解答题
(本小题满分10分)如图,一次函数y1=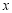 +1的图象与反比例函数
+1的图象与反比例函数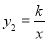 (k为常数,且k≠0)的图象都经过点A(m,2)。
(k为常数,且k≠0)的图象都经过点A(m,2)。

(1)求点A的坐标及反比例函数的表达式;
(2)结合图象直接比较:当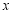 >0时,
>0时,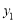 与
与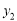 的大小。
的大小。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com